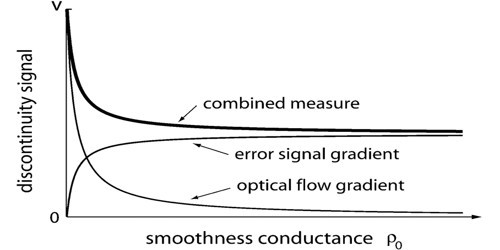
The gradient measures how steep a curve is. Gradient (Slope) of a Straight Line. On a graph of the function, it is the slope of the tangent of that curve. Gradients can be calculated by dividing the vertical height by the horizontal distance. The Gradient (also called Slope) of a straight line shows how steep a straight line is. More generally, it is a vector that points in the direction in which the function grows the fastest. Its coordinates are partial derivatives of that function. A gradient is another word for “slope”. The higher the gradient of a graph at a point, the steeper the line is at that point. At a given point on a curve, the gradient of the curve is equal to the gradient of the tangent to the curve. A negative gradient means that the line slopes downwards. The derivative (or gradient function) describes the gradient of a curve at any point on the curve.
The gradient of a slope (Slope percentage is calculated in much the same way as the gradient. Convert the rise and run to the same units and then divide the rise by the run.)
- A gradient is a measure of how steep a slope is.
- The greater the gradient the steeper a slope is.
- The smaller the gradient the shallower a slope is.
The gradient is a fancy word for derivative or the rate of change of a function. It’s a vector (a direction to move) that. Points in the direction of greatest increase of a function (intuition on why). The gradient of a function is called a gradient field.