Noise Equivalent Count Rate Nuclear Camera

PET stands for Positron Emission Tomography. It is the most latest and powerful radiotracer imaging technique in the field of medical science for imaging to diagnosis various diseases such as tumor, cancer, Parkinson’s disease etc. It is also uses in monitoring response after therapy in the study of new pharmaceutical drugs, and in studying engineering processes .

A positron emission tomography (PET) scan produces a three-dimensional image of functional processes of organs in the body. This functional imaging technique has been used for the last few decades in many clinical applications . It also used in studying engineering processes  and in the study of new pharmaceutical drugs ^.

This chapter outlines the various physical and instrumental features such as PET principles, PET radionuclides, beta decay, annihilation photons, interaction with matter, coincidence detection of annihilation photons, detector selection, acquisition mode, etc.

PET   Principles

In clinical applications, a very small amount of labeled compound (called radiopharmaceutical or radiotracer) is introduced into the patient usually by intravenous injection and after an appropriate uptake period, the concentration of tracer in tissue is measured by the scanner.

At some point, in time the isotope will decay with the emission of a positron. The proton rich isotope achieves stability through positron decay by converting a proton to a neutron. During its decay process, the radionuclide emits a positron which loses its kinetic energy by interactions with the surrounding atoms of the imaged tissue.

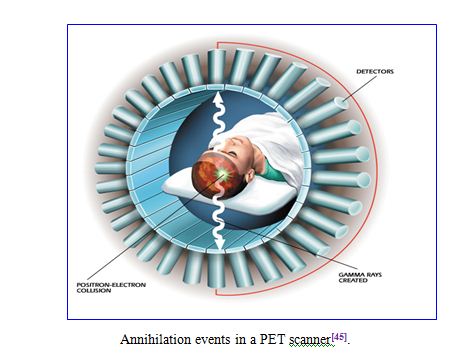
When the positron reaches thermal energy after traveling an extremely tortuous path of 3-5 mm, it encounters an electron from the surrounding atoms (occurs annihilation) [Fig.1.1] and a meta-stable intermediate species called positronium may form .

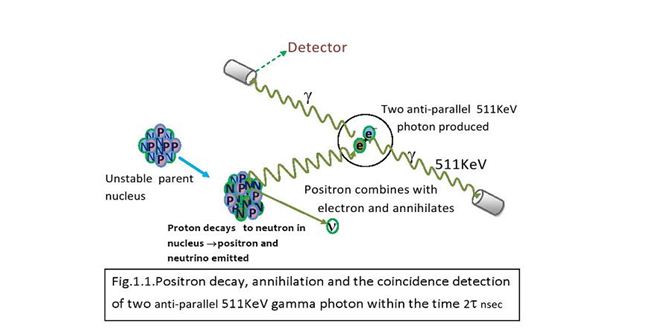
The two particles (electron and positron) combine and “annihilate” each other resulting in the emission of two gamma rays of   511 keV each in opposite directions.

Thus, after annihilation, generally two photons having equal energy of 511keV are produced and emitted nearly back-to-back. The energy of the annihilation photons hit opposite detectors they deposit energy due to scatter and absorption within the detectors. The source (nuclear decay point) is assumed to lie on the straight line (known as the Line of Response) joining the two detector positions by detecting a large number of coincidence events, the distribution  of tracer can be determined by two important fundamental degrading factors in resolution correspond to positron range and annihilation photon.

Line of Response (LOR)

A line joining the centres between two opposite individual detectors is known as a line of response (LOR). It is the line linking the points of detection of two gamma rays.

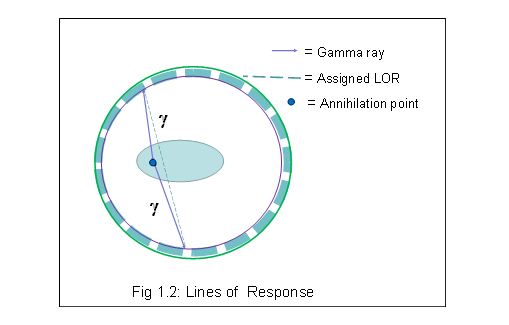Since the detectors have a finite size the LOR is in practice a tube with similar radius. Different LORs must traverse different thicknesses of tissue.

A PET scanner records counts as coincidence events (simultaneous detection of two annihilation gamma rays) between opposite pairs of crystals. Unscattered photon pairs are located for a specific LOR within a thin volume centred on the LOR. The shape of this volume is an elongated parallelepiped, and is called a tube of response (TOR) .The TOR is a function of crystal size. Wide TORs result in poor resolution reconstruction, but with lower noise level. On the other hand, thin TORs will enable the reconstruction to recover higher frequencies which results in an increase of the noise level.

Effect of   Positron Range  

Before undergoing annihilation the positron travels a finite distance. The spatial resolution of PET imaging is limited by positron range of the isotope of interest, off-axis detector penetration linear or angular directions for the image reconstruction process . This positron range contributes an offset between the LOR of two unscattered photons and the positron decay  point . The range of positrons in tissue is an important limitation to the ultimate spatial resolution achievable in positron emission tomography.

Uncertainty in the localization of the decaying nucleus arises due to the positron range which increases with increasing positron initial energy. This uncertainty arises because we wish to determine the location of the Positron decay point, not the annihilation point. The average distance of the LORs from the decay point due to the positron range  in water/tissue is about 0 .2 mm for the positrons emitted from ¹⁸F,whereas this range is increased to 1.2mm for the positrons emitted from ¹⁶O ^[11].

Acollinearity

Annihilation photon acollinearity is a fundamental but little investigated problem in positron emission tomography (PET) ^[12].The angle between the  paths of annihilation photons is not always exactly 180 degree but is typically around 179.5°.This angular deviation of  about 0.5° ^[13] causes a positional error in locating the true annihilation point [Fig.1 .4]. At the time of annihilation, both positron and electron do not come to a complete rest, because they have some non-zero momentum before undergoing annihilation. For the conservation of momentum of the positron-electron pair, the annihilation photons are not emitted exactly in opposite directions.

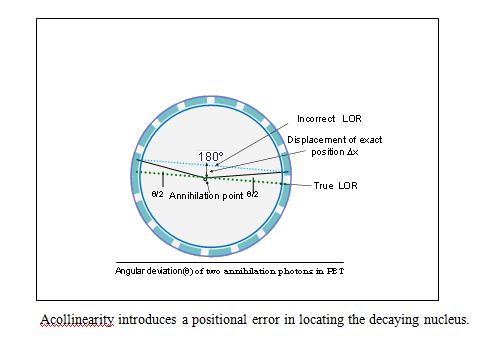The angular deviation causes a separation (Dx) of the LOR from the true annihilation point, which blurs the PET images. This blurring is an increasing function of the detector ring diameter (D) and it causes the maximum effect at the centre of the field of view. The blurring coefficient relating Dx to the ring diameter (D) in calculations of the PET spatial resolution was experimentally determined, i.e., the value of Dx was estimated to be (0.00243± 0.00014)×D for the human subject ^[12]. The acollinearity introduces an uncertainty to the image resolution which is about 1 mm for a 50 cm and about 2 mm for a 100cm ring inner diameter PET tomography .

PET   Radionuclides

A nuclide is a general term applicable to all atomic forms of an element. Nuclides are characterized by the number of protons and neutrons in the nucleus, as well as by the amount of energy contained within the atom. A radionuclide is an unstable form of a nuclide. They may occur naturally, but can also be artificially produced.

The PET technique has developed on the basis of   positron emitting radionuclides, usually produced from a cyclotron. Radionuclides used in PET scanning are typically isotopes with short half-lives such as carbon-11 (T_1/2≈ 20 min), nitrogen-13 (T_1/2≈ 10 min), oxygen-15(T_1/2≈ 2 min), and fluorine-18 (T_1/2≈ 110 min).Positron emitters such as ¹⁸F, ¹⁵O, ¹³N and ¹¹C can be attached  to biological molecules of interest and injected  intravenously. That means radionuclides are incorporated either into compounds normally used by the body such as glucose (or glucose analogues), water, or ammonia, or into molecules that bind to receptors or other sites of drug action.

Currently, ¹⁸F is widely used in PET as the labeled compound FDG (fluorodeoxy glucose) ^[15].Glucose has an increased uptake in malignant cells. FDG is a biologically active molecule which does not affect the normal biological process in the body when administered in tracer quantities.

The mean ranges of positrons and their energies from major positron   .emitting radionuclides.

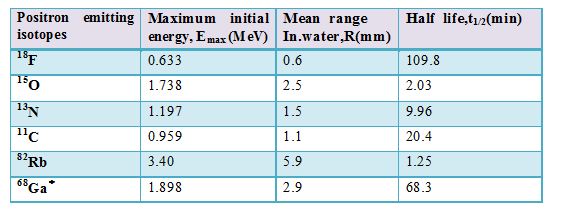⁶⁸Ga is the daughter nuclide of ⁶⁸Ge and is often eluted from a Ge/Ga-68 generator system.⁶⁸Ge has a half life of 270 days.

Such   label led compounds are known as radiotracers. It is important to recognize that PET technology can be used to trace the biologic pathway of any compound in living humans (and many other species as well), provided it can be radio labeled with a PET isotope. Some commonly used PET isotopes and their associated properties are shown in Table-1.1 and the process of positron emission from the unstable radio-nuclides described the following three sections.

Nuclear Decay

An atom consists of nucleus (made of protons and neutrons), and a cloud of electrons around the nucleus. A proton has a positive electrical charge, an electron has an equal negative charge, a neutron is neutral. Protons and neutrons have almost exactly the same mass (weight). An atom generally has an equal number of protons and electrons, and is neutral in charge because of this. The electrons determine the chemical properties and color of the atom. The nucleus determines the mass of the atom, and whether or not it is radioactive.

Let’s take a normal nucleus, carbon-12. This nucleus is made up of 6 protons and 6 neutrons. Together they give this nucleus a mass of 12. Carbon-12 is abbreviated as ¹²C. Another kind of carbon nucleus is carbon-14 (¹⁴C). This one has 6 protons and 8 neutrons. Since an atom normally has an equal number of protons and electrons, these two nuclei have the same number of electrons, and have the same chemical properties (they both act like carbon). ¹⁴C has too many neutrons. An excess of neutrons or protons in a nucleus causes nuclear instability.

This nucleus tends to be stable with emission of radiation, i.e.  ¹⁴C is radioactive and it decays. There are three main ways that a nucleus can decay. It can lose an alpha particle (a helium nucleus) ⁴He, it loses two protons and two neutrons. Or it can lose a negative beta particle, which is the same as an electron, when a neutron converts into a proton. Or it can lose a positive beta particle, which is also called a positron, and is the same as a positive electron, and a proton converts into a neutron.

The nucleus tends to stability through a transition to the lowest possible state for its nucleon number, and the process is known as nuclear beta decay. Beta decay is relevant to the PET technology, and some of its associated features are described below.

Beta  Decay

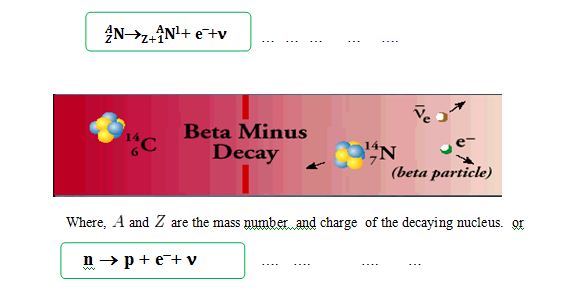
Beta decay is a type of radioactive decay in which a beta particle (an electron or a positron) is emitted from an atom. There are two types of beta decay, positive beta decay(_­­­­­b⁺) and negative beta decay (_­­­­­b^–)  is an example of weak interaction ^[16]. Beta decay does not change the nucleon number but changes the charge only, as detailed in Eq. l.l & 1.2

β⁻ decay  process

The process, in which a neutron converted into a proton and electron with the emission antineutrino, is called   β⁻ decay process. β^– decay generally occurs in neutron-rich nuclei.

β⁺ decay process

The process in which a proton converted into a neutron and positron with the emission neutrino, is called β⁺ decay process. this process is also known as “positron emission” decay. Here actually β decay  occurs through the transformation of a neutron into a proton or vice versa through what is called “the Weak Nuclear Force” or “Weak  interaction

Positron Emission

Positron emission (a type beta decay i.e. β^+ decay) occurs when the neutron to proton ratio in the nucleus is too small and causes nuclear instability Positron emission or beta plus decay (β⁺ decay) is a particular type of radioactive decay, in which a proton is converted to a neutron, and it releases a positron and a  neutrino. As an example, the following equation describes the beta plus decay of carbon-11 to boron-11, emitting a positron and a neutrino.

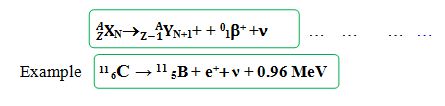In β⁺ decay, a proton is converted into a neutron via the weak nuclear force. Beta emission is accompanied by the emission of a neutrino which shares the missing energy and momentum of the decay.

The neutrino is an electrically neutral particle having no appreciable mass, and is produced in some nuclear reactions such as beta decay, but it is very hard to detect. This light particle interacts with other particles very weakly, and can easily pass through matter without any appreciable interaction. The neutrino is not directly relevant to PET imaging, but its presence in the positron decay makes the energy of the positron variable instead of a fixed energy for a particular isotope.

 In beta decay the change in binding energy appears as the mass energy and kinetic energy of the beta particle, the energy of the neutrino and the kinetic energy of the recoiling daughter nucleus. The energy of an emitted beta particle from a particular decay can take on a range of values because the energy can be shared in many ways among the three particles while still obeying energy and momentum conservation .

 In principle, positron decay is always accompanied by electron capture. The nucleus captures an electron which basically converts a proton to a neutron.  Electron capture (EC) is a decay mode for proton-rich isotopes and often occurs when there is not enough energy to emit a positron.

The energy emission depends on the isotope that is decaying; e.g. 0.96 MeV applies only to the decay of carbon-11. Isotopes which increase in mass under the conversion of a proton to a neutron or which decrease by less than 2m_e, do not spontaneously decay by positron emission.

Nuclei which decay by positron emission may also decay by electron capture. For low-energy decay, electron capture is energetically favored by 2m_ec² = 1.022 MeV, positron emission is forbidden and then the only decay mode is electron capture. In the electron capture process, the nuclide changes into a new element because the proton converts into a neutron ⁸³Rb would have only electron capture decay mode to ⁸³Kr. A proton in the nucleus captures an electron (usually from the K- or L-shell), and forms a neutron and a neutrino.

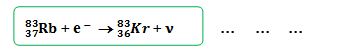When an inner shell electron is captured by the nucleus the atom loses an electron and the atom is left in an excited state. To fill the vacancy, an electron in an outer shell falls into the inner shell gap, releasing energy as an x-ray.

Branching   Ratio or Branching Fraction

In general, the branching ratio (BR) for a particular decay mode is defined as the ratio of the number of atoms decaying by that decay mode to the number decaying in. total,

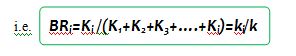Where, BR₁=K₁/K , BR₂=K₂/K

In particle physics and nuclear physics, the branching fraction for a decay is the fraction of particles which decay by an individual decay mode with respect to the total number of particles which decay.

 It is equal to the ratio of the partial decay constant to the overall decay constant. Sometimes a partial half-life is given, but this term is misleading due to competing modes it is not true that half of the particles will decay through a particular decay mode after its partial half-life. The partial half-life is merely an alternate way to specify the partial decay constant λ, the two being related through:

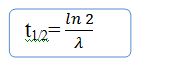 For example, for spontaneous decays of ¹³²Cs, 98.1% are β⁺ decays, and 1.9% are β⁻ decays.

PET scanner detects only 511 kev photons. Different isotopes used in PET have variable fraction of other decay events, which are not detected by PET. This has to be taken into account when calibrating the scanner and the blood samples by dividing the measured

values by the branching ratio.

Branching  ratios for PET  isotopes

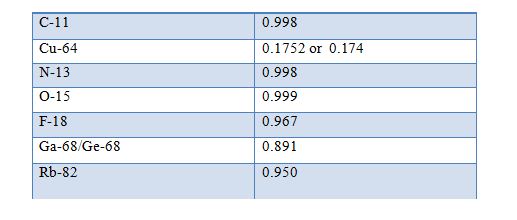
However, invent data branching factor 0.174 is used

Interaction of   Photons with Matter

When a highly penetrating photon interact with matter, the possible interaction processes that occur depending on the energy of the photon, are  

1. Coherent (Coherent) scattering (predominates in human tissue,~< 50keV);
2. Photoelectric effect (< 100 keV);
3. Compton effect (  >100KeV   to ( ~ <2MeV);
4. Pair production ( ≥1.002 MeV);
5. Triplet   production (≥ 2.044 MeV); and
6. Photonuclear   production ( ≥10MeV);

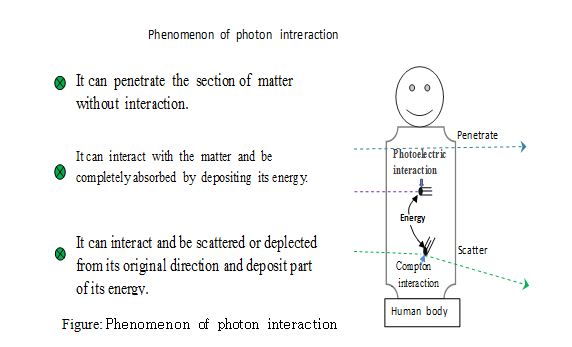In the PET detection process, annihilation photons are completely absorbed by the detectors, mainly through Compton scattering followed by photoelectric absorption. The mechanism of the interactions with matter is briefly outlined below.

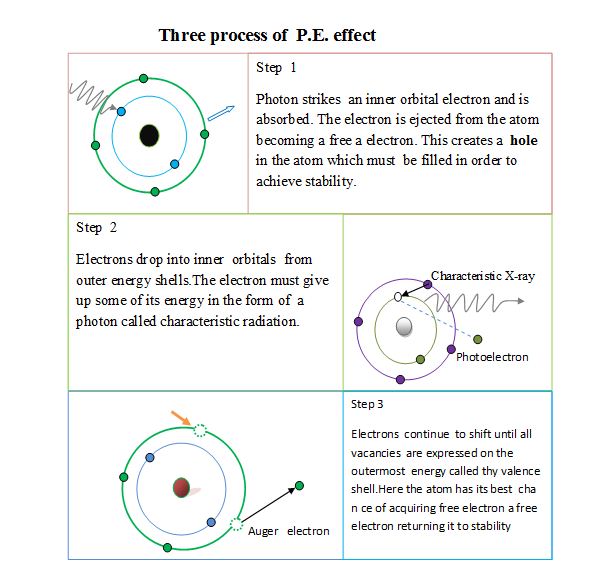
Photoelectric   Absorption The absorption of an X-ray or ¡-ray photon by an atom of the   absorbing material causes the emission of an electron from one of its bound shells. This process is known as photo electric absorption.

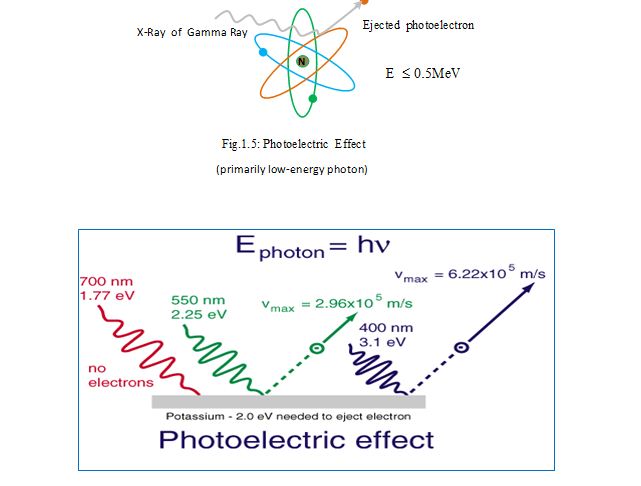In this process, the incident photon completely disappears and its energy is transferred to the orbital electron, the electron gain some kinetic energy because the photon energy is higher than the electron binding energy.  Most of the energy is required to overcome the binding energy of the orbital electron and the remainder imparted to the electron upon its ejection.

The ejected free electron is called a photoelectron which travels a short distance in tissue and is absorbed. The atom’s resultant charge is +1 due to the electron void.

Subsequently, electrons from outer orbital drops inward to fill the void, such as from the L-shell to the K-shell and from the M-shell to the L-shell, etc.

As electrons drop into inner shells they give up energy in the form of an x-ray photon called a characteristic ray.

The energy of this photon will be different in binding energies between the upper (higher energy) shell and the lower shell. If this excess energy is greater than or equal to the binding energy of another electron, then this energy can be used to free the second electron. This secondary electron is called Auger electrons.

The three products of the P.E. effect:

          1) A negative ion (photoelectron),

          2) Characteristic radiation, and

          3) Auger electron results in a positive ion (atom deficient one electron).

There are four simple rules governing the probability of the photoelectric effect occurring :

The incident photon must have sufficient energy to overcome the binding energy of the electron. For example, if a K-shell electron has a binding energy of 70 keV and the incident photon have energy of 68.5 keV, it absolutely cannot eject that..electron from its orbital.

A photoelectric interaction is most likely to happen when the energy of the incident photon exceeds but is relatively close to the binding energy of the electron it strikes. Using our example of a K-shell electron with a binding energy of 68.5 keV, a photoelectric interaction is more likely to occur when the incident photon is 70keV than if it were 120keV.This is because the photoelectric effect is inversely proportional to approximately the third power of energy.

The probability of photoelectric absorption increase sharply with increasing Z (atomic number of the target material) and decreases sharply with increasing incident photon energy..

The tighter an electron is bound to its atom, the more likely it is to be involved in a P.E. interaction. Atoms with high atomic number bind their electrons tighter than atoms with low Z number. These high atomic number elements are more likely to undergo P.E reactions. The probability of the P.E. effect is nearly proportional to the third power of the atomic number.

The fact that P.E. interaction is 1/E³ explains, image contrast decreases when higher x-ray energy are used in imaging. At energies <50keV, P.E. effects plays an important role in imaging soft tissue. It can be used to amplify differences in attenuation between tissues with slightly different atomic numbers, and improves image contrast. e.g: 1) different target and filters in mammography, and 2) use of phosphors containing rare earth elements(lanthanum and gadolinium) in intensifying screens.

The ejection of an electron occurs closer to the nucleus (usually from the K-shell) because the nucleus is involved to conserve the momentum. The benefit of photo electric absorption in x-ray transmission imaging is that there are no additional non-primary photons to degrade the image

Compton Scattering

Compton scattering is an interaction of a high energy incident photon with a loosely bound orbital electron. The binding potential of the loosely   bound electron is small compared to the incident photon energy.

An incident photon with relatively high energy strikes a free outer shell electron, ejecting it from its orbit (inelastic interaction).The photon is deflected by the electron so that it travels to a new direction as scatter radiation.. In this interaction, the photon transfers some of its energy to the electron and deviates from its initial path, and the electron (known as a Compton recoil electron) becomes completely free from the atom

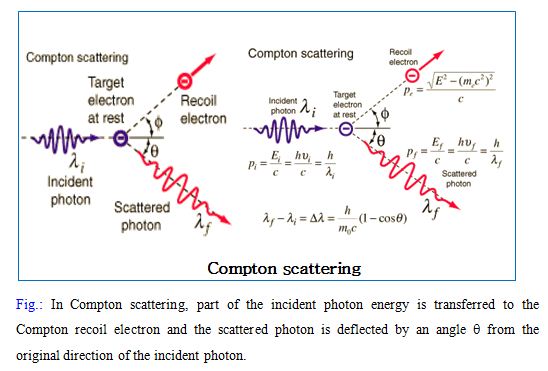The kinetic energy of the “recoil” electron equals the energy lost by the photon, with assumption that the binding energy of the electron is negligible. After interaction, the photon energy is reduced and can be calculated by the well-known Compton formula

Two factors determine the amount of energy that the photon retains, its initial energy and its angle of deflection of the recoil electron.

Compton   scattering is a type of scattering that X-rays and gamma rays undergo in matter. The inelastic scattering of photons in matter results in a decrease in energy (increase in wavelength) of an X-ray or gamma ray photon, called the Compton Effect. Change of wave length can be obtained by following equation,

The interaction between electrons and high energy  photons (comparable to the rest energy of the electron, 511 keV) results in the electron being given part of the energy (making it recoil), and a photon containing the remaining energy being emitted in a different direction from the original, so that the overall momentum of the system is conserved. If the photon still has enough energy left, the process may be .repeated. Almost all scatterred radiation in X and ¡ rays between 30keV to 30MeV interact in soft  tissue by Compton scattering….

Qualitatively, this equation shows that the scattered x-ray energy becomes smaller as the scattering angle increases and, at higher incident energies, this effect is amplified. Compton scattered x-rays can deleteriously affect image quality by reducing contrast and are implicated for environmental radiation protection concerns.

Coincidence Events in PET Detection Process

If two photons are detected within the resolving time t of the system, then the scanner records an event and the event is  referred to as a coincidence event [Fig.1.6]. Since the order of the photons is irrelevant, this gives a coincidence timing window of length 2t

In a PET camera, each detector generates a timed pulse when it registers an incident photon. These pulses are then combined in coincidence circuitry, and if the pulses fall within a short time-window, they are seem to be coincident. A conceptualized diagram of this process is shown in figure

All of the coincidence events detected during an imaging period are recorded by the PET computer system as a raw data set, the coincidence data in PET is reconstructed by a computer to produce cross-sectional images in the axial and coronal planes

Four types of coincidence events are observed in the PET which are given below:

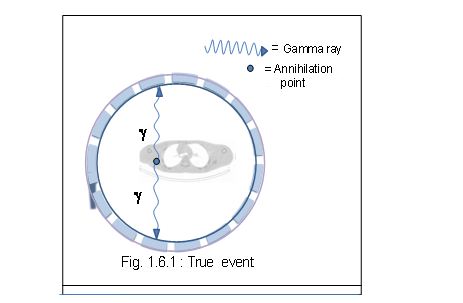
True Events

True coincidences occur when both photons from an annihilation event are detected by detectors in coincidence, neither photon undergoes any form of interaction prior to detection, and no other event is detected within the coincidence time-window.

Or A true event corresponds to detecting two photons arising from an annihilation event which have not appreciably interacted with the imaging object before reaching the detectors.

A true coincidence is an event that derives from a single positron–electron annihilation. The two annihilation photons both reach detectors on opposing sides of the tomography without interacting significantly with the surrounding atoms and are recorded within the coincidence timing window

The sensitivity of a tomography is determined by a combination of the radius of the detector ring, the axial length of the active volume for acquisition, the total axial length of the tomography, the stopping power of the scintillation detector elements, packing fraction of detectors, and other operator dependent settings (e.g. energy window). However, in general terms the overall sensitivity for true  events are given by  eqn

Where Z is the axial length of the acquisition volume, D is the radius of the ring.

Random   Events

A random (or accidental) coincidence occurs when two nuclei decay at approximately the same time .This events  sometimes  referred to as an accidental coincidence arises mistakenly from two separate positron annihilations. After annihilation of both positrons, four photons are emitted. Two of these   photons from different annihilations are counted within the timing   window and are considered to have come from the same positron, while the other two are lost. Two photons from two unrelated decays are detected within the scanner resolving time and the scanner produces a false coincidence event

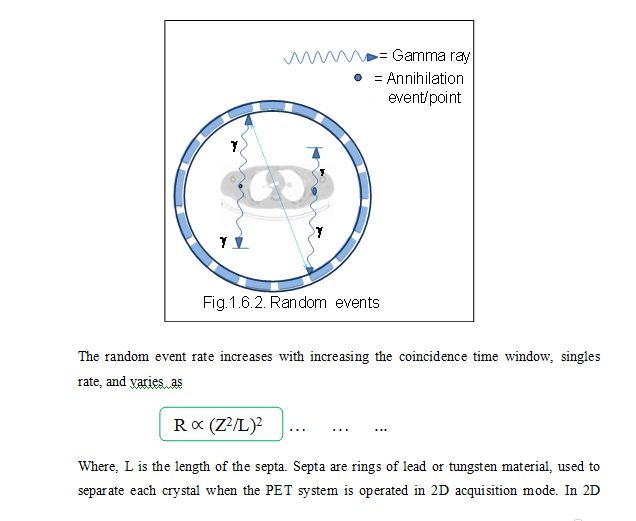mode, coincidences are only recorded between detectors within the same ring or very closely neighboring rings. These events are initially regarded as valid, prompt events, but are spatially uncorrelated with the distribution of tracer. This is clearly a function of the number of disintegrations per second, and the random event count rate (R_ab) between two detectors a and b is given by the following equation

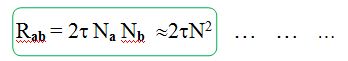
Where Na, Nb are the singles event rate incident upon the detectors a and b, and 2t is the coincidence window width. Usually Na=Nb so that the random event rate increases approximately proportionally to N².

This relation is true provided that the singles rate is much larger than the rate of coincidence events, and that the singles rates are small compared to the reciprocal of the coincidence resolving timet, so that dead-time effects can be ignored.

There are two common methods for removing random events:

• estimating the random event rate from measurements of the single event rates using the above equation, or
• employing a delayed coincidence timing window.

The number of random coincidences detected, depends on the volume and attenuation characteristics of the object being imaged, and on the geometry of the camera. The distribution of random coincidences is fairly uniform across the FOV, and will cause isotope concentrations to be overestimated if not corrected for random coincidences also add statistical noise to the data.

The random coincidence contribution may also be estimated by introducing a delay in one of the coincidence channels. In this technique, timing signals from one detector are delayed by a time significantly greater than the coincidence resolving time of the circuitry. Activity outside the field of view (FOV) can also give rise to random coincidences, so the random rate can be reduced by shielding out of field activity and by reducing the resolving time of the scanner.

Scattered   Events

A scattered coincidence is one in which at least one of the detected photons has undergone at least one Compton scattering event prior to detection. Scattered events arise when one or both of the photons from a single positron annihilation detected within the coincidence timing window have undergone a Compton interaction.

In practice, most scattered photons are scattered out of the field of view and are never detected. Those annihilations for which one or both gamma rays are scattered but still detected are referred to as scattered events.

Since the direction of the photon is changed during the Compton scattering process, it is highly likely that the resulting coincidence event will be assigned to the wrong LOR. The LOR assigned to the event is uncorrelated with the original annihilation event, i.e., an incorrect LOR is formed because the photons’ paths are not collinear

Scattered coincidences add a background to the true coincidence distribution which changes slowly with position, decreasing contrast and causing the isotope concentrations to be overestimated. They also add statistical noise to the signal. The number of scattered events detected depends on the volume and attenuation characteristics of the object   being imaged, and on the geometry of the camera. The contribution of scattered events is described b y

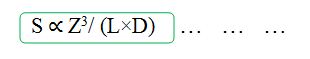
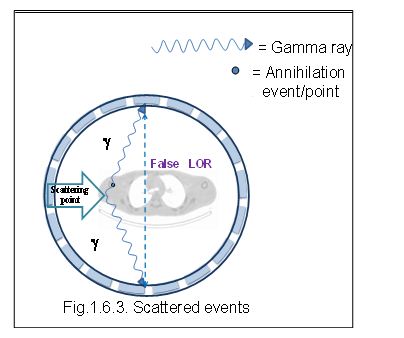As in Fig. 1.6 .3, the event   is incorrectly positioned on the detectors, and hence the effect is to add a broad background to the images. This causes errors in the radiotracer concentration by misplacing-events during reconstruction. Therefore, scattered coincidences degrade both image quality (due to loss of contrast) and quantitative accuracy .

Scattering  in PET can  arise from  three major  sources  namely  inside  the  object, detector  itself, the gantry and  surrounding  environment this also depends on  other factors   such  as object size, density, acceptance  angle,  energy discriminator settings , radiotracer  distribution, etc.  Scattered events can be reduced by using   inter-plane septa and also applying a simple energy   threshold.

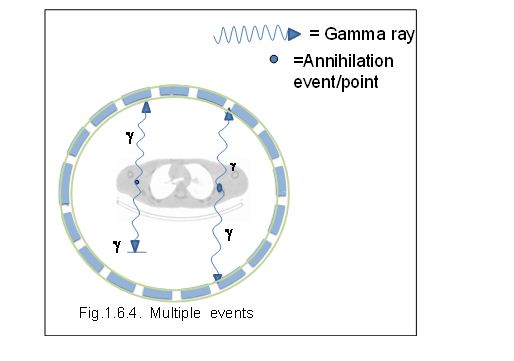
Multiple Events 

These are mainly triple detection events. Multiple (or triple) events are similar to random events, except that three events from two annihilations are detected within the coincidence timing window. Due to the ambiguity in deciding which pair of events arises from the same annihilation, the event is disregarded. Again, multiple event detection rate is a function of count rate;

Multiple coincidences occur when more than two photons are detected in different detectors within the coincidence resolving time. In this situation, it is not possible to determine the LOR to which the event should be assigned, and the event is rejected. Multiple coincidences can also cause event   miss-positioning.

Historical Background of a PET

The idea of PET technology was first evolved when the nature of the positron and the positron decay was known. Positron was first experimentally discovered   by Paul AM Dirac and Carl Anderson in 1932. For their contributions to the discovery of the positron they  won Nobel prizes.

PET is a relatively recent technology, but the principle has been understood for half a century. In the development of PET technology, many scientists from various disciplines have been involved  for more than 50 years. The first application of PET  technology in medicine was  made at  Massachusetts General Hospital (MGH) in  l951 using a simple brain prove  and  two  opposite  NaI (TI) detectors.

lmage reconstruction techniques for  single  photon  tomography developed  in the early 1960s  and about a decade later Chesler of MGH physics group developed the filtered  back projection ( FBP) technique. The first commercial PET scanners were developed in the late 1960’s and used analog electronics to generate tomographic (sliced) images

In 1961, James Robertson and his associates at Brookhaven National Laboratory built the first single-plane PET scan, nicknamed the “head-shrinker’’.

The RAH (RoyalAdelaideHospital’s) investigated this technology in 1968 for bone scanning, but found it too slow and inefficient for clinical use, and difficult to source the isotope.

In the 1970s PET scanning was formally introduced to the medical community and it soon became clear to many of those involved in PET development that a circular or cylindrical array of detectors was the logical next step in PET instrumentation and more sensitive detectors and tomographic capabilities began to appear. The first commercial PET scanner, the ECAT II, introduced in the late 1970s, was capable of brain imaging and could accommodate the torso of a narrow patient .

Although many investigators took this approach, James Robertson and Z.H. Cho were the first to propose a ring system that has become the prototype of the current shape of PET. At that time it was seen as an exciting new research modality that opened doors through which medical researchers could watch, study, and understand the biology of human disease. These scanners were still limited to single regions, but improvements continued, with better   resolution, and  movement from the research area to clinical use.

The first ring tomography was built at Brookhaven National Laboratory in 1973(Robertson JS 1973) and also Michael E Phelps built his first PET tomography, known as PETT I, at WashingtonUniversity in the same year. These first two efforts were unsucce in producing   proper reconstructed images due to lack of various correction techniques. Later on, Phelps and Holfman presented their design of a hexagonal array of 24 NaI (TI) detectors with some correction techniques and image reconstruction algorithms.

In 1973-74, Phelps and his team built a scanner with a diameter of 50 cm which had 24 NaI (TI) detectors known as PETT Il. In late 1974, Mike Phelps and Ed Hoffman at WashingtonUniversity built another scanner with the same diameter for human studies, known as PET III, using 48 NaI (TI) detectors. The scanner provided all the correction  techniques  and an image reconstruction algorithm and a dedicated computer which had all of these capabilities  including gantry movement. After the development of PET III, the  first  commercial  PET  scanner  was  constructed, named ECAT, using 96 NaI (TI)  detectors with a diameter of 3705mm  and was first delivered to the University of California, Los Angeles in 1976.

In 1976, the radiopharmaceutical fluorine-18-2-fluoro-2-deoxyglucose (FDG), a marker of sugar metabolism with a half-life of 110 minutes, enabled tracer doses to be administered safely to the patient with low radiation exposure. The compound was first administered to two normal human volunteers by Abass Alavi in August 1976 at the University of Pennsylvania.

Brain images obtained with an ordinary (non-PET) nuclear scanner demonstrated the concentration of FDG in that organ. Later, the substance was used in dedicated positron tomographic, scanners, to yield the modern procedure.

During the 1980s the technology that underlies PET advanced greatly. Commercial PET scanners were developed with more precise resolution and images. As a result, many of the steps required for producing a PET scan became automated and could be performed by a trained technician and experienced physician, thereby reducing the cost and complexity of the procedure. Smaller, self-shielded cyclotrons were developed, making it possible to install cyclotrons at more locations.

NaI(TI) is still widely used in nuclear medicine gamma cameras  as  standard scintillator  to detect  the 140keV gamma photons from ^99mTc decay. In the detection of 511 keV annihilation photons NaI(TI)  scintillator has some disadvantages due to its low  stopping  power. .Also the manufacturer faces problems in construction due to its hygroscopic  nature. Scintillators with higher density and hence greater stopping power were investigated, including bismuth germinate oxyorthosilicate (BGO), gadolinium orthosilicate (GSO), and barium fluoride (BF), among others and to overcome the  problem bismuth  germinate (BGO) ,which has high stopping power and hence high detection efficiency for 511keV photons, was first introduced  as  a scintillator of choice for PET. The evolution of BGO for  use  in PET  was reported  in the late 1970s A commercial PET brain tomograph using a high density scintillator (BGO), with at least a tentative intended clinical market niche, was introduced in 1978 . Commercial BGO block based PET scanner have been manufactured since 1981. The recent advance of new faster scintillators such as GSO and LSO blocks  faste electronics as well as statistically-based reconstruction algorithms have significantly  improved  the performances of PET scanners for clinical studies.

The recent development of combined PET/CT scanners providing functional and anatomical information has further reduced the lengthy scanning time by avoiding the need for a transmission  scan.

Over the last several years, the major advance in this technology has been the combining of a CT scanner and a PET scanner in one device. The modern PET/CT scanner allows a study to be done in a shorter amount of time but still provides more diagnostic information. By the mid-1990’s, PET had become an important diagnostic tool. In the early 1990s, a new generation of full ring BGO commercial tomographs was introduced . Australia established its first PET facilities, including cyclotrons, in 1992 at the Royal Prince Alfred Hospital, Sydney and Austin Hospital Melbourne.

The Royal Adelaide Hospital’s Facility is the 6^th dedicated PET facility in Australia and saw its first PET patient in September 2000.  The PET/CT scanner, attributed to Dr David Townsend and Dr Nutt was named by TIME Magazine as the medical invention of the year  in 2000

In March 2005 a PET scanner with integral CT was installed at the RAH. The Philips Gemini PET/CT combines a 16 slice Computerised Tomography scanner with a high resolution PET scanner to allow image fusion and improved  localization of  lesions. PET and PET/CT are widely available today. The technology is robust and provides high quality  images. Some of the earlier roadblocks to having  or using a PET or PET/CT device, such as availability of particular  radiopharmaceuticals are no longer present.

Importance of PET Scan

A PET scan is an integral part of the diagnosis, management, and treatment of serious disease. A single PET scan can provide information that once would have required many medical studies, and it can do so without the surgery or other invasive procedures that might otherwise have been required.

PET scans often reveal disease before it can be seen with other tests. Often, in addition to imaging the disease, it can provide information used to determine the most promising treatment methods. PET scans are also used to evaluate how well treatments are working and can often show significant changes far sooner than other tests.

Scintillation Detectors in PET

Scintillation detectors are the most common and successful mode for detection of 511 keV photons in PET imaging due to their good stopping efficiency and energy resolution. These detectors consist of an appropriate choice of crystal (scintillator) coupled to a photo-detector for detection of the visible light. This process is outlined in further detail in the next two sections,

1. Scintillation Process and
2. Crystals Used in PET.

Scintillation  Process

The electronic energy states of an isolated atom consist of discrete levels as given by the Schrodinger equation. In a crystal lattice, the outer levels are perturbed by mutual interactions between the atoms or ions, and so the levels become broadened into a series of allowed bands. The bands within this series are separated from each other by the forbidden bands. Electrons are not allowed to fill any of these forbidden bands. The last filled band is labelled the valence band, while the first unfilled band is called the conduction band. The energy gap, Eg, between these two bands is a few electron volts in  magnitude .

Electrons in the valence band can absorb energy by the interaction of the photoelectron or the Compton scatter electron with an atom, and get excited into the conduction band. Since this is not the ground state, the electron de-excites by releasing scintillation photons and returns to its ground state.

Normally, the value of Eg is such that the scintillation is in the ultraviolet range. By adding impurities to a pure crystal, such as adding thallium to pure NaI (at a concentration of ~1%), the band structure can be modified to produce energy levels in the prior forbidden region. Adding an impurity or an activator raises the ground state of the electrons present at the impurity sites to slightly above the valence band, and also produces excited states that are slightly lower than the conduction band.

Keeping the amount of activator low also minimizes the self-absorption of the scintillation photons. The scintillation process now results in the emission of visible light that can be detected by an appropriate photo-detector at room temperature. Such a scintillation process is often referred to as luminescence. The scintillation photons produced by luminescence are emitted isotropically from the point of interaction. For thallium-activated sodium iodide (NaI(Tl)), the wavelength of the maximum scintillation emission is 415 nm, and the photon emission rate has an exponential distribution with a decay time of 230 ns. Sometimes the excited electron may undergo a radiation-less transition to the ground state. No scintillation photons are emitted here and  the process is called quenching.

Crystals  used in  PET

1.  There are various types of detectors, such as
2. Sodium iodide doped with thallium (NaI (Tl)),
3. Bismuth germanate Bi₄Ge₃O₁₂ (BGO),
4. Lutetium oxyorthosilicate doped with cerium Lu₂SiO₅: Ce (LSO),
5. Yttrium oxyorthosilicate doped with cerium Y₂SiO₅: Ce (YSO),
6. Gadolinium oxyorthosilicate doped with ceriumGd₂SiO₅: Ce (GSO), and
7. Barium fluoride (BaF₂).

There are four main properties of a scintillator which are crucial for its application in a PET detector. They are:

1. The stopping power for 511 keV photons,
2. Light output,
3. Signal decay time, and
4. The intrinsic energy resolution.

 The stopping power of a scintillator is characterized by the mean distance (attenuation length = 1/μ) travelled by the photon before it deposits its energy within the crystal.

A short attenuation length provides maximum efficiency in counting 5l1keV photons. A scintillator with high Z_eff  and density(r) provides increased stopping power. High Z is good because it increases the probability of photoelectric interactions within the crystal to absorb all the energy .Bismuth Germanate (BGO) has been used as a PET detector of choice for the last few decades due to its high stopping power and because it possesses a relatively high Z_eff  and density. Approximately, 95% of the annihilation photons undergo interaction. In a 3-cm thick BGO block detector. whereas only 36% of the photons undergo interaction within a 3-cm thick NaI detector.

The detector should have a capability of producing high light output so as to have better energy resolution(ΔE/E).The better energy resolution provides a sharp peak and hence increases the chance to discriminate against the scatter events. However, in practice it is usually impossible to identify small angle scatters in this way. In scattering through 30⁰ a 5l I keV photon loses just l2% of its energy, so that it is not possible to discriminate scatter through angles much less than 30⁰ using a scintillator such as BGO. Lutetium-ortho-oxysilicate (LSO) based block detectors provide high light output compared to BGO and hence allow improved energy resolution.

A high light-output scintillator affects a PET detector design in two ways:

1. It helps achieve good spatial resolution with a high encoding ratio (ratio of number of resolution elements, or crystals, to number of photo-detectors) and
2. attain good energy resolution.

Good energy resolution is needed to efficiently reject events which may Compton scatter in the patient before entering the detector. The energy resolution (ΔE/E) achieved by a PET detector is dependent not only upon the scintillator light output but also the intrinsic energy resolution of the scintillator. The intrinsic energy  resolution of a scintillator arises due to inhomegeneities in the crystal growth process as well as non-uniform light output for interactions within it.

 The energy resolution values given in this table are for single crystals. In a full PET system, variations between crystals and other factors such as light readout due to block geometry contribute to a significant worsening of the energy resolution. Typically, NaI (Tl)detectors in a PET scanner achieve a 10% energy resolution for 511 keV photons, while the BGO scanners have system energy resolution of more than 20%.NaI (Tl) provides very high light output leading to good energy and spatial resolution with a high encoding ratio.

The slow decay time leads to increased detector dead time and high random coincidences. A shorter scintillation decay time enables faster production of the signal after complete absorption of the photon. The fast scintillators allow the use of a narrow coincidence time window which reduces the probability of detection of random events. Another consideration in a PET detector is dead time which is a main limiting factor at high count rates. A short decay is required to process each pulse individually at high activity level. The light output of BGO is fairly poor compared to the NaI detector. B GO has a longer decay time constant, and hence increased dead time which limits the count rate performance of the scanner.LSO has a shorter decay time constant so as to have reduced dead time and allow the use of a shorter coincidence time window which is appropriate to reduce the random events at high count rates.

However, the excellent stopping power of BGO gives it high sensitivity for photon detection in PET scanners. Currently, commercially produced whole-body scanners have developed along the lines of advantages and disadvantages of these two individual scintillators. The majority of scanners employ BGO and, when operating in 2D mode, use tungsten septa to limit the amount of scatter by physically restricting the axial field-of-view imaged by a detector area. This results in a reduction of the scanner sensitivity due to absorption of some photons in the septa.

The low light output of BGO also requires the use of small   photo-multiplier tubes to achieve good spatial resolution, thereby increasing system complexity and cost. NaI(Tl)), the overall energy resolution of LSO is not as good as NaI(Tl). This is due to intrinsic properties of the crystal.

Lanthanum bromide (LaBr₃) has recently been developed at Delft University and can be used as a cost effective scintillator but its only drawback is low stopping power . LaBr₃ provides better energy resolution than LSO, CsF  and BaF2, and hence it allows the use of a narrow energy window to reduce scatter events. In addition, it has an improved timing characteristic that allows the use of a short coincidence timing window to reduce efficiently the random events.

Gadolinium oxyorthosilicate (GSO) scintillator has been used by some research groups for whole-body, brain and animal scanner designs . GSO scintillator has some useful physical properties for PET detectors. One advantage of GSO over LSO, in spite of a lower stopping power and light output, is its better energy resolution and more uniform light output. Commercial systems are now being developed with GSO detectors.

Extremely fast scintillators, such as BaF₂, have found use in time-of-flight PET scanners during the last few years. Since BaF₂ has a very low stopping power, time-of-flight scanners have a reduced sensitivity leading to lower SNR. Time-of-flight positron emission tomography (TOF PET) using CsF_2, scintillator developed to a limited extent in the l980s but in scintillators such as LSO and GSO etc have recently renewed interest in TOF PET scanners among the PET research community . Table [ 1.3 ] summarizes the physical properties of some common scintillators that are currently used in various PET scanners.

Acquisition    Mode

A PET scanner is usually operated in acquisition mode . there are some scanner  which can be operated in both 2D and 3D mode by extending or retracting septa. When septa are extended the scanner allows only data for direct and adjacent planes to be collected. Septa reduce most of the scatter events and also, reduce photon flux from out side the field of view (FOV), but block many true events, and hence limit the scanner sensitivity. Septa reduces the sensitivity of the detector by 40% or more as they have significant shadowing effect on the detectors.

There are 2n-1 image planes in 2D acquisition mode. where n is the number of crystal  rings.

As the septa are retracted in 3D mode the PET detection efficiency increases by collecting all coincidence events. In 3D acquisition mode all possible LORs within the FOV are acquired. This improves the image quality even when the administered dose is relatively low and also reduces the over alls scanning time.

The large contribution of scattered events in 3D PET is the major degrading factor of image quality. Scatter from outside the field of view also contributes to the PET raw data which increases the detector dead time and the random events. In 3D PET, the scatter events may contribute 20-50% or more. whereas in 2D their contribution is usually less than l5% in a 16-ring tomography. Also, 3D acquisition mode gives a non uniform axial sensitivity profile which is 30 time higher in the centre of the scanner compared to the end planes whereas the 2D mode leads to a very nearly profile profile following a biomodal pattern . In multiring tomographs direct planes are formed between detectors in. the. same.ring.and.cross.planes.are.formed.between.neighboring.rings.in.2D.acquisition Mode.

Objective  of  this thesis work

PET is the most recent nuclear technology by which 3D functional image can be constructed of live organ. It is usually used to detect the malignant cell. At present cancer is a threat for all the people of the world. A large number of people of the world are suffering from cancer. PET can detect the malignant cell at the beginning of cancer. Till now cancer treatment are not available, which can cure a man perfectly. Usually cancer is detected at the extremum stage but PET scan can detect the malignant cell at the very early stage of cancer. Beside this PET scanner used in industrial sector to examine their products quality and also used in pharmaceuticals. So, PET scanner is very important for our modern life.

The image quality of PET scanner depends on some of its characteristics. Such as spatial resolution, sensitivity and noise equivalent count rate (NECR). When a PET scanner is installed it is necessary to check the above characteristics of PET. NECR is the most important measure of  PET scanner image quality. It is frequently used for the acceptance of testing a PET machine.

The objective of the work is to study the NECR of a nuclear PET camera. Since PET has been introduced in Bangladesh in the last 2 years, it has been renewed interest about its extremum uses with safety. As it uses the radioactive tracer, nuclear safety should be maintained properly. Keeping this in mind, this work has been intended. This work will be helpful for the people to impact proper knowledge about the uses of PET scan with safety. Besides this, it will intend the new researchers for further development about safety, which will greatly escorts to the cancer treatment in Bangladesh.

The most sophisticated part of a PET or PET-CT installation is the cyclotron. Cyclotron is one kind of charge particle accelerator. In PET imaging it requires proton rich isotopes such as ¹⁸F, ¹⁵O, etc. The Cyclotron used to produce such radioactive isotopes which are used to make the functional images of the body. So, cyclotron is mandatory for PET system.

This chapter includes various types of accelerators, circular or cyclic accelerators, cyclotron physics, history of cyclotron, principle operation of cyclotron, production of ¹⁸F isotope, etc.

Accelerator 

A particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams.

There are two basic classes of accelerators:

1. Electrostatic Accelerators and
2. Oscillating field Accelerators.

Electrostatic Accelerators

Electrostatic accelerators use static electric fields to accelerate particles. A small-scale example of this class is the cathode ray tube in an ordinary old television set. Other examples are the Cockcroft–Walton generator and the Van de Graaf generator. The achievable kinetic energy for particles in these devices is limited by electrical breakdown.

Oscillating field Accelerators

Oscillating field accelerators, on the other hand, use radio frequency electromagnetic fields and circumvent the breakdown problem. This class, which development started in the 1920s, is the basis for all modern accelerator concepts and large-scale facilities. Rolf Widerøe, Gustav Ising, Leó Szilárd, Donald Kerst and Ernest Lawrence are considered as pioneers of this field, conceiving and building the first operational linear particle accelerator,^[2] the betatron, and the cyclotron ^[59]. Because colliders can give evidence on the structure of the subatomic world, accelerators were commonly referred to as atom smashers in the 20th century . Despite the fact that most accelerators (but ion facilities) actually propel subatomic particles, the term persists in popular usage when referring to particle accelerators in general.

Linear particle accelerators

In a linear accelerator (linac), particles are accelerated in a straight line with a target of interest at one end. They are often used to provide an initial low-energy kick to particles before they are injected into circular accelerators. The longest linac in the world is the Stanford Linear Accelerator, SLAC, which is 3 km (1.9 mi) long. SLAC is an electron-positron collider.

modern superconducting, multicell linear accelerator component

Circular or cyclic accelerators

In the circular accelerator, particles move in a circle until they reach sufficient energy. The particle track is typically bent into a circle using electromagnets. Example of circular accelerator are Cyclotrons, Betatrons, Synchrotrons etc.

The advantage of circular accelerators over linear accelerators (linacs) is that the ring topology allows continuous acceleration, as the particle can transit indefinitely. Another advantage is that a circular accelerator is smaller than a linear accelerator of comparable power (i.e. a linac would have to be extremely long to have the equivalent power of a circular accelerator).

Depending on the energy and the particle being accelerated, circular accelerators suffer a disadvantage in that the particles emit synchrotron radiation. When any charged particle is accelerated, it emits electromagnetic radiation and secondary emissions. As a particle traveling in a circle is always accelerating towards the center of the circle, it continuously radiates towards the tangent of the circle. This radiation is called synchrotron light and depends highly on the mass of the accelerating particle.

Introduction to Cyclotrons

A circular particle accelerator in which charged atomic or subatomic particles generated at a central source are accelerated spirally outward in a plane perpendicular to a fixed magnetic field by an alternating electric field is known as cyclotron. A cyclotron is capable of generating particle energies between a few million and several tens of millions of electron volts ^[65]. It is a machine for accelerating charged nuclear particles, commonly protons, so that they may be used to probe the nuclei of target atoms. Such “atom smashers” are considered the microscopes of nuclear physics.

Cyclotrons have a single pair of hollow ‘D’-shaped plates to accelerate the particles and a single large dipole magnet to bend their path into a circular orbit. An alternating electric field between the dees continuously accelerates the particles from one dee to the other, while the magnetic field guides them in a circular path. This means that the accelerating D’s of a cyclotron can be driven at a constant frequency by a radio frequency (RF) accelerating power source.

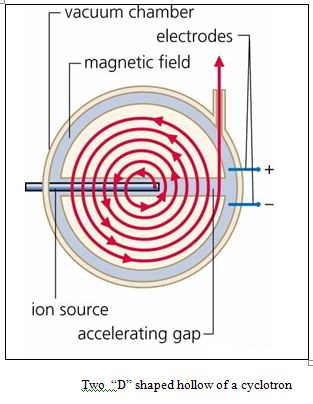As the speed of the particles increases, so does the radius of their path, and the particles spiral outward. In this manner, a cyclotron can accelerate protons to energies of up to 25 million electron volts.

The modern cyclotron uses two hollow D-shaped electrodes held in a vacuum between poles of an electromagnet. A high frequency AC voltage is then applied to each electrode.

In the space between the electrodes an ion source produces either positive or negative ions depending on the configuration. These ions are accelerated into one of the electrodes by an electrostatic attraction, and when the alternating current shifts from positive to negative, the ions accelerate into the other electrode. Because of the strong electromagnetic field, the ions travel in a circular path. Each time the ions move from

one electrode to another they gain energy, their rotational radius increases, and they produce a spiral orbit. This acceleration continues until they escape from the electrode.

The accelerated particles are extracted from the cyclotron when they reach the end of the spiral acceleration path. This beam of accelerated subatomic particles can be used to bombard a variety of target materials to produce radioactive isotopes.

Various isotopes are used in medicine as tracers that are injected into the body and in radiation treatments for certain types of cancers. Cyclotrons are also used for research purposes in academic and industrial settings, and for positron emission tomography (PET).

The particles are injected in the centre of the magnet and are extracted at the outer edge at their maximum energy.

Cyclotrons reach an energy limit because of relativistic effects whereby the particles effectively become more massive, so that their cyclotron frequency drops out of synch with the accelerating RF. Therefore simple cyclotrons can accelerate protons only to an energy of around 15 million electron volts (15 MeV, corresponding to a speed of roughly 10% of c), because the protons get out of phase with the driving electric field.

If accelerated further, the beam would continue to spiral outward to a larger radius but the particles would no longer gain enough speed to complete the larger circle in step with the accelerating RF. To accommodate relativistic effects the magnetic field needs to be increased to higher radii like it is done in isochronous cyclotrons. A magnet in the synchrocyclotron at the Orsay proton therapy centre.

An example for an isochronous cyclotron is the PSI Ring cyclotron which is providing protons at the energy of 590 MeV which corresponds to roughly 80% of the speed of light. The advantage of such a cyclotron is the maximum achievable extracted proton current which is currently 2.2 mA. The energy and current correspond to 1.3 MW beam power which is the highest of any accelerator currently existing.

History of Cyclotron

In the nineteenth century, some physicists still labored under the theory-really, the dream of alchemists for centuries that elements could be made to transmute into other elements through chemical processes.

In 1902, Ernest Rutherford and Frederick Soddy explained the new phenomenon of radioactivity as a “transformation” of one element into another, occurring spontaneously in nature; and in 1919, Rutherford succeeded in deliberately causing transmutations by bombarding light elements with the alpha particles emitted from naturally decaying radio-elements.

Since very few of the projectile alpha particles collided with nuclei of the target atoms, the number of transmutations was relatively small. Therefore, scientists sought new ways to increase the number of projectile particles and to accelerate them to higher energies. The copious production of charged particles was the easier task, the high-voltage engineering required for acceleration proved far more difficult.

Scientists tried a number of different approaches to the acceleration problem, including a voltage multiplier circuit (Sir John Douglas Cockcroft and Ernest Walton) and an electrostatic generator (Robert J. Van de Graaff), both linear accelerators.

E. O. Lawrence and his graduate students at the University of California, Berkley tried many different configurations of the cyclotron before they met with success in 1929.

In 1930, Ernest O. Lawrence, with the help of one of his students, M. Stanley Livingston, designed and constructed the first of many magnetic resonance accelerators . where it was first operated in. Lawrence’s accelerator operated at voltages much lower than other machines, yet imparted as much or more energy to its projectiles.

 Lawrence won the Nobel Prize for Physics for his work on the cyclotron in 1939.

The D’s of Lawrence’s first cyclotron were only about 4 inches (10 cm)  in diameter. The accelerating chamber of the first cyclotron measured 5 in (12.7 cm) in diameter and boosted hydrogen ions to energy of 5-45 MeV depending on the settings. One mega electron volt (MeV) is 1.602 × 1013 Joule.

Subsequent models of 9, 11, 27, 37, and 60 inches followed, with a new model built almost every other year. These larger machines surpassed an early goal of one million electron volts projectile energy; many different types of atoms were split; and scores of new radioisotopes were identified, including the first trans-uranium elements.

The first European cyclotron was constructed in Leningrad in the physics department of the Radium Institute, headed by Vitali Khlopin. This instrument was first proposed in 1932 by George Gamow and Lev Mysovskii and was installed and running by.

Principle of operation of a Cyclotron

The cyclotron, destined to be the chief tool of nuclear physics, worked on the principle that charged particles, accelerated across a voltage gap, travel in a circular path under the influence of a magnetic field. It is used for accelerating positive ions, so that they acquire energy large enough to carry out nuclear reactions.

 If confined to a hollow disk-shaped chamber built in two D-shaped halves (called “D’s”) and if subjected to a radio-frequency voltage alternation as the particle passes from one half to the other, the particle receives two accelerations per cycle and travels at higher velocities in ever-larger circles. In a cyclotron, the positive ions cross again and again the same alternating electric field and thereby gain the energy.

An alternating electric field attracts the particles from one side of the cyclotron to the other. The cyclotron’s magnetic field, generated by the two electromagnets, bends each particle’s path into a horizontal spiral, forcing it to accelerate in order to keep up with the alternating electric field. When the particle reaches its peak acceleration it is released to collide with the desired target, producing observable nuclear reactions.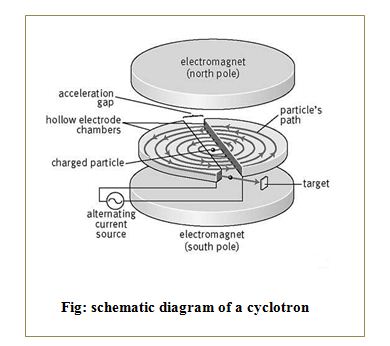It is based on the principle that a positive ion can acquire sufficiently large energy with a comparatively smaller alternating potential difference by making them to cross the same electric field time and again by making use of a strong magnetic field.

A positively charged particle is released at the center of the gap at time t = 0. It gets attracted towards the Dee, which is at a negative potential at that time. It enters the uniform magnetic field between the Dees perpendicularly and performs uniform circular motion in the gap. As there is no electric field inside the Dees, it moves on a circular path of radius depending upon its momentum and comes out of the Dee after completing a half circle.

As the frequency of A.C. (fA) is equal to fc, the diameter of the opposite Dee becomes negative when the particle emerges from one Dee and attracts it with a force, which increases its momentum. The particle then enters the other Dee with larger velocity and hence moves on a circular path of larger radius.

This process keeps on repeating and the particle gains momentum and hence radius of its circular path goes on increasing but the frequency remains the same. Thus the charged particle goes on gaining energy, which becomes maximum on reaching the circumference of the Dee. When the particle is at the edge, it is deflected with the help of another magnetic field, brought out and allowed to hit the target. Such accelerated particles are used in the study of nuclear reactions, preparation of artificial radioactive substances, treatment of cancer and ion implantation in solids.

Types of  Cyclotron 

Commercially available biomedical cyclotrons can be divided in four categories depending on their energy :

 Sub-Low Energy;

• < 12MeV
• Simens Eclipse 11MeV (RDS111)
• IBA Molecular Cyclone 10, 10 MeV
• GE Healthcare Minitrace, 9.5 MeV

Low energy;

1. 15 to 20 MeV
2. Advanced Cyclotron Systems TR-19, variable energy 13 to 19 MeV
3. GE Healthcare PETtrace, 16.5 MeV
4. IBA Molecular Cyclone 18, 18 MeV

Medium Energy;

• 20 to 25 MeV
• Advance Cyclotron Systems TR-24, 24 MeV

High Energy;

• 25 to 30 MeV
• Advance Cyclotron Systems TR-30, 31 MeV
• IBA Molecular Cyclone 30, 30 MeV

Cyclotron for PET

 Medium energy cyclotron is much better than low or sub-low energy cyclotrons for clinical and research applications. Medium energy cyclotron  are much more efficient at making PET isotopes other than Fluorine. Low energy machine were basically designed to produce only fluorine. Above 20MeV the cyclotron can be used for both PET and SPECT isotopes.

Properties of cyclotron of cyclotron

Cyclotron property depends on the following parameters:

Beam

Medium and Vbariable Energy for PET, SPECT and research isotopes;

1. Ions: Extracted (H+, D+)
2. Accelerated (H+, D+)
3. Ion source external                      :  ECR, polarizes IS
4. Ion source internal                       :  hot cathode hooded arc
5.  Norm.emittance hor./ver.              :  204/1.2 p mm mrad
6. Phase width                                 :  160-400
7. Energy Spread (fwhm)                 :  ~ 0.3%
8. Beam current                               :  ~ 200mA or higher

High beam transmissios  at high current limit.

Magnetic Structure

1. Number of symmetry period
2.          (sectors)                                           : 4-12
3. Radially varying sector angle               : 20-60 degrees
4. Hill field                                           : ~2 Tesla
5. Vally field                                         : ~0.2 Tesla

Dee Structure

1. Number of Dees                                :  2
2. Position                                            :  Inside the system
3. Dee voltage (nominal)                        :  6 kW

RF System

• Max.accel.voltage                          :  2 ×70 Kv
• Frequenvy                                      :  5-17 MHz, 520MHz
• Powerful vacuum system for beam transmission.

Vacuum System

1. Low operating vacuum pressure at high current limit.
2. Vacuum system category including the oil free pumps and low operating vacuum.

Cyclotron produced isotopes

Cyclotron produced various types of isotopes such as ¹⁸F, ¹¹C, ¹³N etc. All the isotopes are used as compound radio tracer such as the name of fluorine-18 radio tracer is fluoro-deoxy-glucose and name of carbn-11 radio tracer is methionine, etc. Different types of isotopes, their tracer compound, physiological process and applications are given in the following.

Production of ¹⁸F isotope

 Introduction

Naturally occurring fluorine is monoisotopic. However a number of radioactive isotopes of fluorine such as ¹⁷F ,¹⁸F, ²⁰F ,²¹F have been produced since 1930’s.All the radioactive isotope of fluorine are man made. ¹⁷F ,¹⁸F have a deficit of neutrons and decay by positron emission. ²⁰F ,²¹F have surfeit  of neutrons and decay by negative beta emission. Only ¹⁸F and ²⁰F have been used in radiotracer in chemical studies.

 Isotopes of fluorine

The half life of ²⁰F radio isotope is 10 sec whereas the half life of ¹⁸F 110 minutes. Because of long half life 18F is very as radio tracer. However, a major limitation is that the production of ¹⁸F and the subsequent experimental work must normally be carried out within 3 or 4 half lives. The 511KeV g-photons resulting from the annihilation of the 0.64MeV positron decay during the decay of ¹⁸F can be easily detected using nuclear detector.

Fluorine-18 is an important   isotope in the radiopharmaceutical industry, and is primarily synthesized into fluorodeoxyglucose (FDG) for use in positron emission tomography (PET scans). It is a fluorine radioisotope which is an important source of positrons. It is substituted for hydroxyl and used as a tracer in the scan. Its significance is due to both its short half-life and the emission of positrons when decaying.

Production of ¹⁸F

Several methods have been used to produce ¹⁸F isotopes and the most commonly used methods are given in the following

In the radiopharmaceutical industry, ¹⁸F is made using either a cyclotron or linear particle accelerator to bombard a target, usually of pure or enriched oxygen-18-water

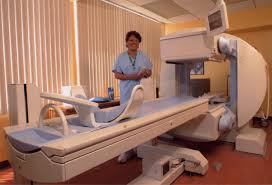
The ECAT 951/31 system, a PET scanner manufactured by Siemens (Siemens-CTI, Knoxville, TN, USA), is designed to produce cross-sectional pictures of radioactive distributions inside patients. The scanner has two bucket rings, each having 16 detector modules (four blocks in a module). All the buckets are housed in a gantry arranged in rings with 100 cm inner diameter giving a 60 cm diameter transaxial field of view (FOV) and 10.8 cm axial FOV.

The even numbered alternate detector modules from a original standard ECAT PET system were used to make the miniPET system with a diameter of 50% of the original. The size of the new geometry was reduced by about half, but the physical shape was the same as the original standard system.

The miniPET system was designed with 2 bucket rings each having 8 detector modules whereas the original system was 2 bucket rings each having 16 modules. Septa and rod sources were not included  in the miniPET, like in the standard system. Therefore, the facility of gantry movement was not available as there were no gantry drives to control the new system. To avoid problems due to the absence of gantry and gantry movement in the new system, the original ECAT software was simplified to control data acquisition directly.

This chapter includes various components of the ECAT 951 PET system and the design architecture of the miniPET.

Description to ECAT (951 series) and its various components

Various components and parameters

The scanner consist of two bucket rings, each ring has 16 detector modules. There are four blocks in a detector module. Each BGO block, viewed by four PMTs, is cut into an 8×8 array of segmented crystal elements, so the scanner has 8192 individual crystal detectors (size 6.25 mm transverse, 6.75 mm axial center-to-centre and 30 mm radial thickness /crystal depth). The BGO block provides high photopeak efficiency for the detection of 511 keV gamma rays and in the ECAT scanner the detection rate is up to 2×10⁶ coincidence events per second.

The spatial resolution of  the ECAT 951 system is about 6 mm in the transaxial direction and 7 mm in the axial direction. All the buckets are housed in a gantry arranged in rings

with 100 cm inner diameter giving a 60 cm diameter transaxial field of view (FOV) and 10.8 cm axial FOV. The gantry allows moving the scanner, which tilts up to ±90º from the horizontal axis and rotates ±45º ^[7] about a vertical axis. The software allows the investigators to develop new algorithms for data acquisition, processing and clinical applications.

The Gantry of the Scanner

 The gantry is the ¢donut¢ shaped part of the scanner that houses houses the buckets and the associated detector electronics, septal ring assemblies, patient alignment lasers, connecting cables, air-cooling systems and three rotating rod sources for the purposes of testing and calibrating the scanner and performing attenuation measurements. But the main job of the gantry is to support and position the detectors perfectly. The 32 detector modules (BGO blocks plus associated bucket electronics) are mounted on the detector support plate. The support plate is joined through two trunion bearings to the main frame. The trunion bearings allow the gantry to tilt for any suitable alignment about the horizontal axis. It also provides a quiet and comfortable environment to position the patients accurately inside the scanner field of view (FOV).

Motions of Gantry

The gantry can be tilted on its bearings about the horizontal axis by up to 30⁰ in both directions (±30⁰) as seen in Fig. 3.1, and can also be pivoted on its base about the vertical axis by ±45⁰. The gantry of the scanner allows the facilities of flexible motions for demanding imaging situations .The gantry allows moving of  the scanner ,which  tilts up to ±90⁰  from the horizontal axis. The motions are driven by motors, and maintained under operator control rather than computer control, by pressing the switches located at the front side of the scanner.

The patient lies on the couch (also known as a table) is moved both in horizontal and vertical direction during examination. The patient couch of the system was designed for comfortable patient support, accurate and precise positioning. The couch top must be capable of moving at least 1800mm to allow the patient to be scanned from ‘head toe’ without having the repositioned. The couch has an adjustable head holder with tilt capability. The patient platforms movement is controlled by computer control and a  dc motor used for its movements. The couch is able  to move in the horizontal direction up to 129 cm and from 75 cm to 104 cm in vertical direction.

Architecture of a the miniPET

Architecture of the miniPET is almost similar as the standard ECAT 951 system. The number of components used in miniPET is half of the components of ECAT 951. Such as instead of 36 detector modules 16 detector modules are used in miniPET. This section

concentrates on the necessary changes for the new scanner design, internal cable connections between various hardware components, operating mode, and coincidence combinations among the detector modules, etc.

The miniPET Scanner Design 

The complete miniPET scanner was designed using 16 detector modules (“buckets”) arranged in two rings. The detector modules were mounted on a horizontal wooden table. The wooden table was used to support the modules as the system had no gantry.

Four blocks, each block (4 PMTs plus crystal matrix) having 64 distinct crystal elements, together with the associated readout electronics comprise one detector module. Therefore, the miniPET system was a 16 ring tomograph having 4096 individual crystal detectors. The axial and transaxial field of view (FOV) of the camera were 10.8 cm and 20 cm diameter.

Shows the layout of the new miniPET camera, where the acquisition and processing units are not included. In the Figure the connecting cables are clearly seen and the functions of the cables are described in the following section. The technical characteristics of the scanner are summarised in

There are many cables required to complete the complicated PET system. Various cables used in different purposes. Four cables are connected to each detector module, these are given bellow.

Clock cable – is used by the detector module to communicate with clock and computer to receive commands, return status information and get timing information.

Data cable –The data cable must be connected to the correct connector on the ring receiver. In miniPET only even  numbered buckets are used, and cables are connected to alternate inputs of the ring receiver.. The data cable also connections between the ring receiver 2 and the upper bucket ring of the system.

PS cable – the power supply (PS) cable is used to supply +5V/-5V to the electronics circuits in the bucket.

HV cable – the high voltage (HV) cable supplies 1500V to the PMTs to accelerate the photoelectrons to the anodes.

Acquisition Mode 

Data acquisition in 2D or 3D mode are possible in the miniPET system by installing the ring differences in the software program. The miniPET scanner  perform all the experiment in 2D mode without any septa. The ring difference is  smaller than or equal to three. i.e.(ring difference ≤3). Thirty one  image planes are formed  in total in the scanner. Among these, 16 direct planes were formed from LORs with ring difference equal to 0 or 2 and 15 cross planes were formed from LORs with ring difference equal to 1 or 3.

Coincidence Issues among the Buckets

In the miniPET camera, the same coincidence combinations as in the original scanner are used, so that each detector module is in coincidence combination with the 6 opposite modules. Of these 6, 3 modules are in the same bucket ring and the remaining 3 are in the other bucket ring . Examples of coincidence combinations recorded among the detector modules of the camera are as follows:

Lower Ring Combinations 

Bucket 0 is in coincidence combination with the detector buckets 6, 8, 10 and bucket 4 with the buckets

Upper Ring Combinations

Bucket 16 is in coincidence combination with the detector buckets 22, 24, 26 and bucket 20 with the buckets.

Combinations for Cross Rings

Bucket 0 in the lower ring is in coincidence combination with detector buckets 22, 24, 26 in the upper ring. Similarly, bucket 4 (in the lower ring) is in coincidence with the buckets 26, 28, 30 (in the upper ring).

The detector bucket 16 in the upper ring is in coincidence combination with the buckets 6, 8, 10 (in the lower ring), bucket 20 (in the upper ring) with the buckets 10, 12, 14 in the lower ring. So, the number of coincidence combinations in one ring is (8×3)/2 = 12. Therefore, the total number of coincidence combinations in the miniPET camera, i.e., four combinations of rings is

                                     12×4 = 48.

 The miniPET Detector System

The miniPET scanner has 4096 individual small crystal detectors which yields 256 detectors in each of 16 axial crystal rings, 64 BGO blocks grouped in 16 detector modules arranged in two buckets rings on the system gantry, and 256 photomultiplier tubes (PMTs). The detailed parameters of the detector system are described separately in the following sections.

BGO Crystal Detector

In the miniPET scanner, bismuth germanate (BGO) crystal is used as a scintillation detector in the form of blocks which are cut into an 8×8 array of crystal elements [Fig. 3.2]. The dimensions of each distinct crystal element are 6.25 mm transverse × 6.75 mm axial (center-to-center spacing) × 30 mm radial (crystal depth).  The slots between crystals are approximately 0.6 mm wide. The detailed characteristics of the BGO scintillation crystal are shown in

Electronics of the Bucket

 The electric signals from the photomultipliers in each block are analyzed for position, time and energy by the bucket electronics, and eventually transferred to the ring receiver for further processing. Three types of “Board” are assembled in each detector module: 1) Analog Signal Processor, 2) Position Energy Processor, and 3) Bucket Controller.

The complete miniPET scanner was designed using 16 detector modules (“buckets”) arranged in two rings. The detector modules were mounted on a horizontal wooden table. The wooden was used to support the modules as the system had no gantry.

NEC was first introduced by Strother et al and was derived from the noise-equivalent-quanta concept, which originates from conventional photographic imaging. Briefly, noise-equivalent quanta describe the equivalent number of quanta or counts required by an ideal imaging system to produce the same noise characteristics as does an actual system that is degraded by noise.

In positron emission tomography (PET), the concept of noise equivalent count rate (NEC) is a measure of image quality. Where NEC describes the equivalent coincidence counting rate that would have the same noise properties as the net true counting rate, corrected for spurious coincidences arising from 2 particular sources: random (accidental) coincidences and scattered events.

NEC is fairly straightforward to measure and has become a standard metric for scanner performance provided by manufacturers and determined as part of acceptance testing for new equipment. NEC is most frequently (or invariably, in the case of acceptance testing) computed using a standard test object. NEC rate used to understand the scanner performance under a wide range of imaging situations, and enables comparisons of count rate taking into account the statistical noise due to scattered and random events. The axial extent of the test object has a large impact on NEC , that varies considerably with scanner design and acquisition mode. According to Watson et al and previously by Lartizien et al. and Townsend et al. the NEC varies for a single patient at different axial positions during a whole-body scan.

Noise Equivalent Count Rate NECR (or NEC rate) is one of the important characteristics of PET/CT instrument. Higher the NEC value indicates better the PET image quality.It has

been shown that the signal-to-noise ratio in the images reflects the global signal-to-noise ratio which, is related to the NEC. Count rate performance can be determined by calculating the noise equivalent count rate (NEC). Due to scatter and randoms in the measured PET data, it is not easy to compare different scanners or the same system operating under different acquisition modes. The noise equivalent count rate is defined as the rate of true coincidences which would (in the absence of randoms and scatters) give rise to the same noise level in the data.  Before the optimum use of a new system it is necessary to measure the scanner characteristics as a function of count rate. The general formula to calculate the NEC rate is

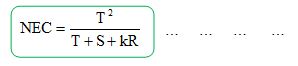where T, S and R are the true, scatter and random rates respectively. The parameter k is the randoms correction factor with a value of 1 or 2 depending on the randoms correction method.

 The value k=1 is used when the randoms contribution is estimated from the singles count rates. A value of 2 is used when randoms are measured using a delayed coincidence window, as in the present work, to account for the additional noise due to the subtraction.

In the work, true, scatter and random events  were measured aiming to test the camera NECR characteristics by taking into account the statistical noise. After designing a PET camera, it is necessary to measure its various characteristics performance.

Materials and Method

To measure the noise equivalent count rate of the system, the same 10 cm diameter polyethylene cylindrical phantom was considered as used previously for the scatter fraction measurement.

The phantom was filled with 1000 ml water and mixed with ¹⁸F having radioactivity 240 MBq. The cylinder was shaken to uniformly mix the ¹⁸F radio isotope into the water. Then the phantom placed at the centre of the scanner. A set of 300 seconds scans was acquired every half hour. These scans were continued for almost 16 hrs.

Randoms were estimated by introducing delay into the coincidence circuit which was an extra 100 ns time delay. Multiples were recorded simultaneously with the prompt and delayed events. The unscattered (True) + scattered events were calculated as the difference between prompt and (random + multiple) events as the formula: T^* = [P – (R + M)], where T^* is the unscattered plus scattered coincidence rate. Scattered and true coincidences were separated from the formulae: S = T^* × (SF) and T = T^* × (1–SF), using the formula of scatter fraction,             we have the value of S=20.63% OF S+T.So, S=.2063 and T=0.7937 from analysis of the sinograms from the scatter phantom. Finally, the noise equivalent count rate was calculated from the above NEC formula (Eqn.4.1). Data Acquisition and Analysis

After positioning the phantom at centre of the scanner the experiment were reapeted for 19 times. NECR or NEC  was calculated from the file named as June26cyl1 at 300sec at 11:45am

All the calculations were repeated 19 times following the calculation of We determine nineteen NEC values and corresponding true, scatterd, random and multiple count rate. All the values are given in the following table.