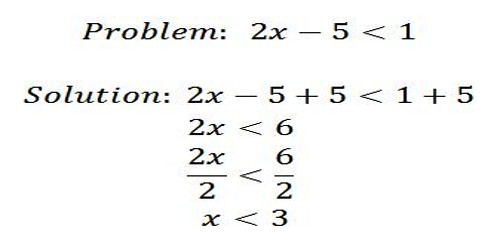Solving an Inequality
An inequality is similar to an equation. There are two expressions separated by a symbol that indicates how one expression is related to the other. In an equation such as 7x = 49, the = sign indicates that the expressions are equivalent. In an inequality, such as 7x > 49, the > sign indicates that the left side is larger than the right side.
To solve the inequality 7x > 49, we follow the same rules that we did for equations. In this case, divide both sides by 7 so that x > 7. This means that x is a value and it is always larger than 7, and never equal to or less than 7.
The “less than” symbol (<) may also be seen in inequalities.
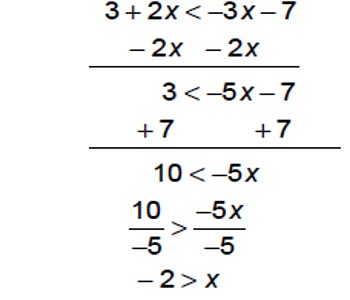
Explanation:
Here is an example: Consider the inequality
When we substitute 8 for x, the inequality becomes 8-2 > 5. Thus, x=8 is a solution of the inequality. On the other hand, substituting -2 for x yields the false statement (-2)-2 > 5. Thus x = -2 is NOT a solution of the inequality. Inequalities usually have many solutions.
As in the case of solving equations, there are certain manipulations of the inequality which do not change the solutions. Here is a list of “permissible” manipulations:
Rule 1. Adding/subtracting the same number on both sides.
Example: The inequality x-2>5 has the same solutions as the inequality x > 7. (The second inequality was obtained from the first one by adding 2 on both sides.)
Rule 2. Switching sides and changing the orientation of the inequality sign.
Example: The inequality 5-x> 4 has the same solutions as the inequality 4 < 5 – x. (We have switched sides and turned the “>” into a “<”).
An inequality such as 3x – 7 < 8 is similar to the equation 3x – 7 = 8. However, this time we are looking for numbers which if you multiply by 3, then subtract 7, you get an answer of less than 8.
Unlike 3x – 7 = 8, which has just one answer, there are lots of numbers for which this is true (in fact, an infinite number). So our answer is not a number, but a range of numbers.
We solve these inequalities just like simple equations: what you do to one side, you must do to the other.
Information Source: