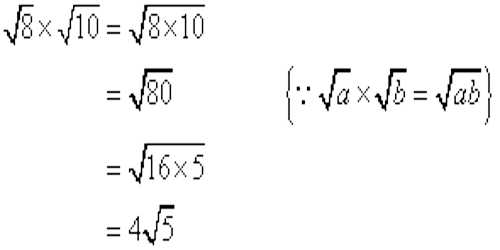Definitions of surds: A root of a positive real quantity is called a surd if its value cannot be exactly determined. It is a number that can’t be simplified to remove a square root (or cube root etc). For example, each of the quantities √3, ∛7, ∜19, (16)^2/5 etc. is a surd.
More Examples:
- √2 (square root of 2) can’t be simplified further so it is a surd
- √4 (square root of 4) CAN be simplified to 2, so it is NOT a surd
Multiplication of Surds
Follow the following steps to find the multiplication of two or more surds.
Step I: Express each surd in its simplest mixed form.
Step II: Observe whether the given surds are of the same order or not.
Step III: If they are of the same order then the required product is obtained by multiplying the product of the rational co-efficient by the product of surd-factors.
If they are of different orders then the product is obtained by the above method after reducing them to surds of the same order.
If different order surds have the same base then their product can easily be obtained using the laws of indices.

Examples of multiplication of surds:
Find the product of 7∜4 and 5∜3
Solution:
The product of 7∜4 and 5∜3
= (7∜4) × (5∜3)
= (7 × 5) × (∜4 × ∜3)
= 35 × 4√(4⋅3)
= 35 × ∜12
= 35∜12
Find the product of 2√12, 7√20 and √32
Solution:
The product of 2√12, 7√20 and √32
= (2√12) × (7√20) × (√32)
= (2√(2⋅2⋅3) × (7√(2⋅2⋅5) × √(2⋅2⋅2⋅2⋅2)
= (4√3) × (14√5) × (4√2)
= (4 × 14 × 4) × (√3 × √5 × √2)
= 224 × √(3⋅5⋅2)
= 224 × √30
= 224√30
Information Source: