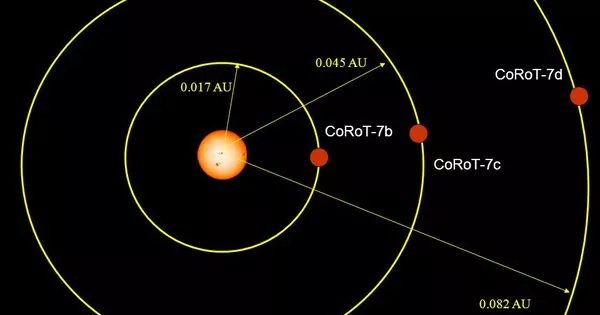
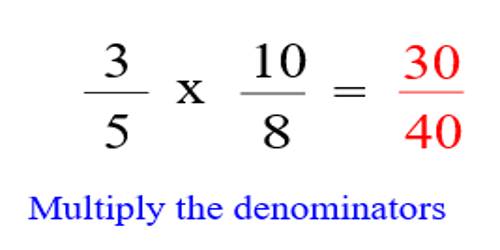Comparing Unlike Fractions
If two fractions have different numerators and denominators it is difficult to determine which fraction is larger. It is easier to determine which is larger if both fractions have the same denominator.
Multiply the numerator and denominator of one fraction by the same number so both fractions will have the same denominator. For example, if 5/12 and 1/3 are being compared, 1/3 should be multiplied by 4/4. It does not change the value of 1/3 to be multiplied by 4/4 (which is equal to 1) because any number multiplied by 1 is still the same number. After the multiplication (1/3 * 4/4 = 4/12), the comparison can be made between 5/12 and 4/12.
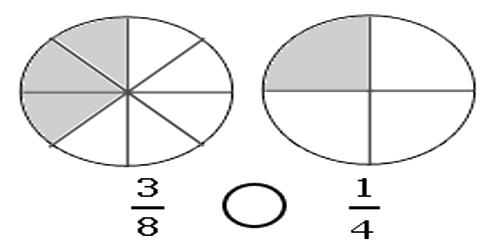
In comparing unlike fractions, we first convert them into like fractions by using the following steps and then compare them.
Step I: Obtain the denominators of the fractions and find their LCM (least common multiple).
Step II: Each fractions are converted to its equivalent fraction with denominator equal to the LCM (least common multiple) obtained in Step I.
Step III: Compare the numerators of the equivalent fractions whose denominators are same.
You may have to multiply both fractions by different numbers to produce the same denominator for both fractions. For example if 2/3 and 3/4 are compared, we need to multiply 2/3 by 4/4 to give 8/12 and multiply 3/4 by 3/3 to give 9/12. The fraction 3/4 which is equal to 9/12 is larger than 2/3 which is equal to 8/12.
The fraction with the larger numerator is the larger fraction if the denominators are the same.
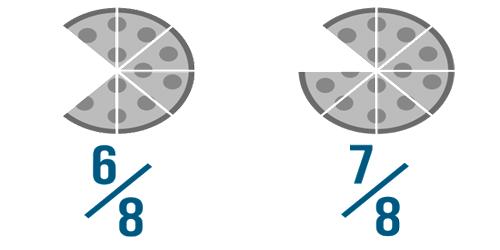
These fractions are unit fractions: Each of them has the same numerator. You can see that as the denominator gets larger, the fraction gets smaller. To order fractions with like numerators, look at the denominators and compare them two at a time. The fraction with the smaller denominator is the larger fraction.
Information Source: