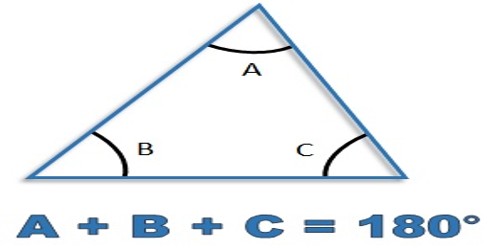
Triangle is a plane figure with three straight sides and three angles. The three angles always add to 180°. The vertex is a corner of the triangle. Every triangle has three vertices. The interior angles of a triangle always add up to 180°. The exterior angles of a triangle always add up to 360°.
Types of triangles based on their angles
- A RIGHT triangle has one 900
- An OBTUSE triangle has one angle that is greater than 900.
- An ACUTE triangle has all three angles less than 900.
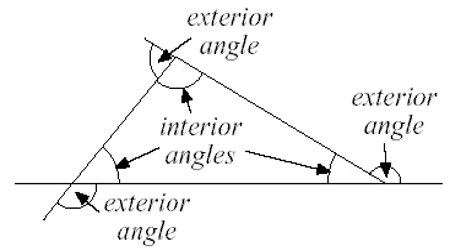
Fig: Angles of a Triangle
Properties of Angles of a Triangle
- The three angles of a triangle are together equal to two right angles.
ABC is a triangle.
Then ∠ZXY + ∠XYZ + ∠YZX = 180°
Using this property, let us solve some of the examples.
Solved examples:
(i) In ∆XYZ, ∠X = 55° and ∠Y = 75°. Find ∠Z.
Solution:
∠X + ∠Y + ∠Z = 180°
or, 55° + 75° + ∠Z = 180°
or, 130° + ∠Z = 180°
or, 130° – 130° + ∠Z = 180° – 130°
Therefore, ∠Z = 50°
(ii) In the ∆XYZ, ∠Y = 5∠Z and ∠X= 3∠Z. Find the angles of the triangle.
Solution:
∠X + ∠Y + ∠Z = 180°
or, 3∠Z + 5∠Z + ∠Z = 180°
or, 9∠Z = 180°
or, 9∠Z / 9 = 180°/9
Therefore, ∠Z = 20°
We know, ∠X= 3∠Z
Now, plug-in the value of ∠Z
∠X= 3 × 20°
Therefore, ∠X= 60°
Again we know, ∠Y= 5∠Z
Now, plug-in the value of ∠Z
∠Y= 5 × 20°
Therefore, ∠Y= 100°
Hence, the angles of the triangle are ∠X = 60°, ∠Y = 100° and ∠Z = 20°.
- If one side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles.
The side QR of the ∆PQR is produced to S.
Then ∠PRS = ∠RPQ + ∠PQR
Corollary 1: An exterior angle of a triangle is greater than either of the interior opposite angles.
In ∆PQR, QR is produced to S.
Therefore, ∠PRS > ∠RPQ and ∠PRS ∠PQR
Corollary 2: A triangle can have only one right angle.
Corollary 3: A triangle can have only one obtuse angle.
Corollary 4: A triangle must have at least two acute angles.
Corollary 5: In a right-angled triangle, the acute angles are complementary.
Information Source: