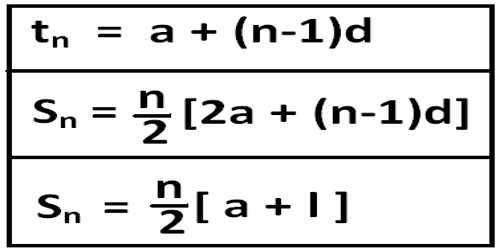A sequence of numbers is known as an arithmetic progression (A.P.) if the difference between the term and the preceding term is always same or constant. An arithmetic progression is a sequence of numbers such that the difference between any two successive members is constant.
For example,
- the sequence 1, 2, 3, 4, … is an arithmetic progression with common difference 1.
- the sequence 3, 5, 7, 9, 11,… is an arithmetic progression with common difference 2.
- the sequence 20, 10, 0, -10, -20, -30, … is an arithmetic progression with common difference -10.
Problems on Arithmetic Progression
Here we will learn how to solve different types of problems in the arithmetic progression.
- Show that the sequence 7, 11, 15, 19, 23, ……… is an Arithmetic Progression. Find its 27th term and the general term.
Solution:
First term of the given sequence = 7
Second term of the given sequence = 11
Third term of the given sequence = 15
Fourth term of the given sequence = 19
Fifth term of the given sequence = 23
Now, Second term – First term = 11 – 7 = 4
Third term – Second term = 15 – 11 = 4
Fourth term – Third term = 19 – 15 = 4
Fifth term – Fourth term = 23 – 19 = 4
Therefore, the given sequence is an Arithmetic Progress with the common difference 4.
We know that nth term of an Arithmetic Progress, whose first term is a and the common difference is d is tn = a + (n – 1) × d.
Therefore, 27th term of the Arithmetic Progress = t27 = 7 + (27 – 1) × 4 = 7 + 26 × 4 = 7 + 104 = 111.
General term = nth term = an = a + (n – 1)d = 7 + (n – 1) × 4 = 7 + 4n – 4 = 4n + 3
- The 5th term of an Arithmetic Progression is 16 and 13th term of an Arithmetic Progression is 28. Find the first term and common difference of the Arithmetic Progression.
Solution:
Let us assume that ‘a’ be the first term and ‘d’ be the common difference of the required Arithmetic Progression.
According to the problem,
5th term of an Arithmetic Progression is 16
i.e., 5th term = 16
⇒ a + (5 – 1)d = 16
⇒ a + 4d = 16 ………………. (i)
and 13th term of an Arithmetic Progression is 28
i.e., 13th term = 28
⇒ a + (13 – 1)d = 28
⇒ a + 12d = 28 ……………….. (ii)
Now, subtract the equation (i) from (ii) we get,
8d = 12
⇒ d = 12/8
⇒ d = 3/2
Substitute the value of d = 3232 in the equation (i) we get,
⇒ a + 4 × 3/2 = 16
⇒ a + 6 = 16
⇒ a = 16 – 6
⇒ a = 10
Therefore, the first term of the Arithmetic Progression is 10 and common difference of the Arithmetic Progression is 3/2.
Information Source: