An ordinary differential equation (ODE) is an equation involving some ordinary derivatives of a function (as opposed to partial derivatives). In comparison to the term partial differential equation that might be in relation to more than one independent variable, the term ordinary is used. An equation relating a function f of one variable to its derivatives is used in mathematics. A linear differential equation is a differential equation defined in the unknown function by a linear polynomial and its derivatives, which is an equation of the form
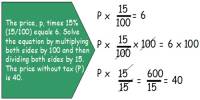
a0 (x)y + a1 (x)y’ + a2 (x)y” + … + an (x)y(n) + b(x) =0,
Where a0 (x), …, an (x) and b(x) are arbitrary distinguishable functions that need not be linear, y ‘,… y(n) are the successive derivatives of the x variable’s unknown feature y.
At each point, the derivative, written f’ or df/dx, of a function f expresses its rate of change, which is how rapidly the function’s value increases or decreases as the variable’s value increases or decreases. The rate of change is simply its slope, expressed as f’ = a, for the function f = ax + b (representing a straight line). For many factors, linear differential equations play a prominent role within ordinary differential equations. Solutions of linear differential equations are the majority of elementary and special functions used in physics and applied mathematics.
Scaling of the Ordinary Differential Equation (ODE)
Solving an ODE is usually more complex than quick integration. Even so, integration is still the essential concept, since we need to go from derivative to function. Typically, deciding what integration we need to do is the hard part. As physical processes are modeled with non-linear equations, linear differential equations are usually approximated for a simpler solution. By translating the equation into an analogous linear ODE, the few non-linear ODEs that can be solved directly are normally solved.
For other functions, the rate of change varies along the function curve, and the topic of differential calculus is the precise way of describing and measuring it. In general, a function’s derivative is again a function, so it is also possible to measure the derivative, (f’)’ or simply f” or d2f/dx2, and it is called the original function’s second-order derivative. It is possible to describe higher-order derivatives similarly. In terms of known functions and integrals, some ODEs can be solved directly. The equation for calculating the Taylor series of solutions may be useful if that is not possible. Numerical methods for ordinary differential equations can provide an approximation of the solution for applied problems.
Many mathematicians, including Newton, Leibniz, the Bernoulli family, Riccati, Clairaut, d’Alembert, and Euler, have studied differential equations and contributed to the field. It is defined that the order of a differential equation is that of the highest order derivative it contains. As the power to which the highest order derivative is increased, the degree of a differential equation is defined. The equation: (f‴)2 + (f″)4 + f = x
It is an example of a differential equation of the second-degree, third-order. Depending on the author and which notation is most suitable for the task at hand, the notation for distinction varies. In this sense, the notation of Leibniz (dy/dx,d2y/dx2,…,dny/dxn) is more useful for differentiation and integration, while the notation of Lagrange (y′, y′′, …, y(n)) is more useful for the compact representation of derivatives of any order, and the notation of Newton is also used in physics to describe low-order derivatives with respect to time. A first-degree equation is considered linear if the first power occurs with the function and all its derivatives and if only the independent variable x is involved in the coefficient of each derivative in the equation.
Since it is much simpler and less error-prone to confirm that a solution satisfies an ODE than solving the ODE, checking the solution is a necessary step in the solution process. Some equations, such as f′ = x2, can be solved by simply remembering which function has a derivative that will satisfy the equation, but the solution is not evident by examination in most cases, and the topic of differential equations is partly to distinguish the various types of equations that can be solved by different techniques.
Information Sources: