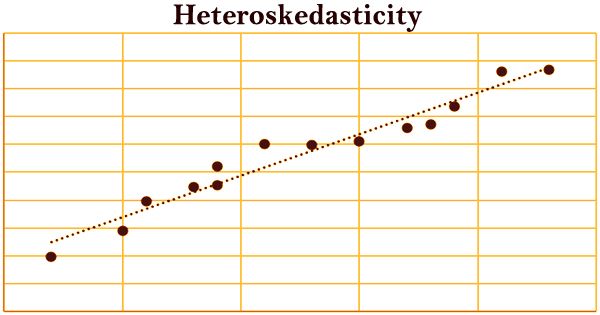
A difficult term to pronounce is heteroskedasticity (or heteroscedasticity), but it doesn’t need to be a difficult definition to understand. It occurs when there are non-constant standard deviations of an expected variable, monitored over various values of an independent variable or as compared to previous time periods. It refers to the situation in which a variable’s variability is disproportionate across the spectrum of a second variable’s values that predicts it. The lack of homoscedasticity is, thus, heteroscedasticity. A common example is the collection of income observations in various cities.
The tell-tale indication upon visual examination of the residual errors with heteroskedasticity is that they will appear to fan out over time. The opposite of heteroscedasticity is homoscedasticity, meaning that the variability of a DV (dependent variable) is equal across IV (independent variable) values. The presence of heteroscedasticity is a significant worry in relapse investigation and the examination of fluctuation, as it negates factual trial of centrality that expects that the displaying blunders all have a similar difference. Heteroscedasticity is most oftentimes talked about regarding the suspicion of parametric investigations (for example direct relapse).
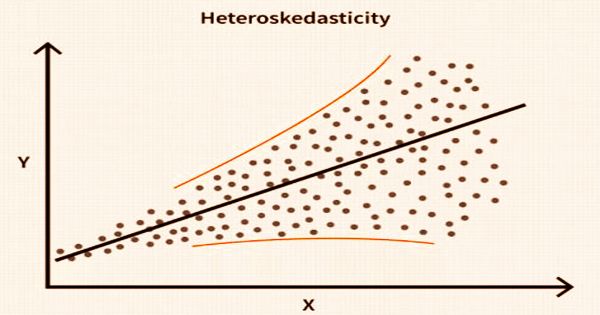
Example of Heteroskedasticity
Because heteroskedasticity is concerned with the perceptions of the second moment of error, its existence is referred to as the second-order misspecification. In two forms, heteroskedasticity often arises: conditional and unconditional.
- Conditional heteroskedasticity defines non-constant volatility correlated with the volatility of the previous cycle (e.g., daily). Stock markets, where volatility today is strongly related to volatility yesterday, are a common application of conditional heteroskedasticity. This model explains periods of high volatility and low volatility that persist.
- Unconditional heteroskedasticity refers to general structural changes in volatility which are not linked to the volatility of the previous period. It is used when it is possible to identify potential high and low volatility cycles. Heteroskedasticity may also refer to cases where the information approaches a boundary; where the variance must necessarily be smaller because the data range is limited by the boundary.
In particular, the disturbances are heteroskedastic if the variance of €i depends on i or on the value of xi. One way they might be heteroskedastic is if σ2i = xiσ2 (an example of a scedastic function), so the variance is proportional to the value of x. Although heteroskedasticity does not cause bias in the estimates of the coefficient, it does make them less accurate; lower accuracy increases the risk that the estimates of the coefficient are farther away from the correct population value. More precisely, it is believed that a regression model’s error (a.k.a residual) is homoscedastic overall values of the DV’s expected value.

Check for heteroskedasticity by examination
In finance, conditional heteroskedasticity is commonly seen within the prices of stocks and bonds. the amount of volatility of those equities can not be predicted over any period. Heteroscedasticity doesn’t cause ordinary statistical method coefficient estimates to be biased, although it can cause ordinary method of least squares estimates of the variance (and, thus, standard errors) of the coefficients to be biased, possibly above or below verify or population variance. The margin of error between data sets, such as predicted results and actual results, can be measured using these differences as it provides a measure of the deviation of data points from the mean value.
However, heteroscedasticity has more extreme implications for any non-linear model (for example, Logit and Probit models): the maximum likelihood estimates (MLE) of the parameters would be skewed as well as inconsistent (unless the likelihood function is changed to correctly take into account the precise form of heteroscedasticity). The opposite of heteroskedastic is homoskedastic; it refers to a condition during which the variance of the residual term is constant or nearly so. it’s needed to make sure that the estimates are accurate, that the prediction limits for the variable quantity are valid, which confidence intervals and p-values for the parameters are valid.
Most of the heteroscedasticity identification techniques described above can be adjusted for use even if the data does not derive from a normal distribution. In certain cases, this hypothesis may be relaxed, giving rise to a test protocol based on the same or similar test statistics but with the distribution tested by alternate routes under the null hypothesis. Heteroskedasticity is a significant idea in relapse demonstrating, and in the venture world, relapse models are utilized to clarify the exhibition of protections and speculation portfolios. The most notable of these is the Capital Asset Pricing Model (CAPM), which clarifies the exhibition of stock as far as its unpredictability comparative with the market in general.
Information Sources: