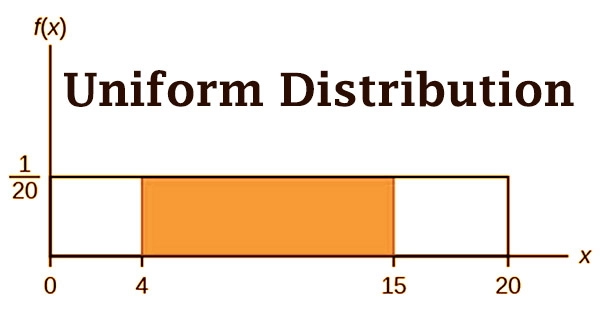
Uniform distribution is a word used in statistics to describe a type of probability distribution in which every conceivable event has an equal chance of occurring. Because the chances of drawing a heart, a club, a diamond, or a spade are equal, a deck of cards has uniform distributions. The probability is consistent since every factor has equivalent possibilities of being the result. A coin likewise has a uniform conveyance on the grounds that the likelihood of getting either heads or tails in a coin throw is something similar.
A coin flip that returns a head or tail has a probability of p = 0.50 and would be represented by a line from the y-axis at 0.50. There are a finite number of outcomes in discrete uniform distributions. A continuous uniform distribution is a factual dispersion with a boundless number of similarly reasonable quantifiable qualities. In an ordinary conveyance, information around the mean happens all the more often.
The ideas of discrete uniform distribution and nonstop uniform distribution, just as the irregular factors they portray, are the establishments of measurable investigation and likelihood hypothesis.
The ideas of discrete uniform distribution and nonstop uniform distribution, just as the irregular factors they portray, are the establishments of measurable investigation and likelihood hypothesis. Uniform distributions are divided into two types: discrete and continuous. A discrete uniform distribution is shown by the different outcomes of rolling a die: it is conceivable to roll a 1, 2, 3, 4, 5, or 6, but not a 2.3, 4.7, or 5.5.
As a result, for each outcome, the roll of a die yields a discrete distribution with p = 1/6. There are just six conceivable outcomes, with nothing in between. The simplest statistical distribution is the uniform distribution. The idea of uniform distribution, just as the arbitrary factors it portrays, structure the establishment of factual investigation and likelihood hypothesis.
For instance, on the off potential for success that you have on a traffic intersection and start to haphazardly hand a $100 greenback to any fortunate individual who strolled by, then, at that point, each bystander would have an equivalent shot at being given the cash. The probability percentage is 1 divided by the entire number of possible outcomes (number of passersby). Short persons and women, on the other hand, would have a better chance of receiving the $100 note than the rest of the crowd. It’s hardly what you’d call uniform probability.
A consistent distribution may also be found in a deck of cards. This is because a person’s chances of drawing a spade, a heart, a club, or a diamond are all identical. One more illustration of a uniform distribution is the point at which a coin is thrown. The probability of getting a tail or head is something similar. The chart of a uniform circulation is typically level, whereby the sides and top are corresponding to the x and y axes.
Rather from being discrete, certain uniform distributions are continuous. A continuous uniform distribution would be an idealized random number generator. A discrete uniform distribution is a statistical distribution with limited values and equal probability of outcomes in statistics and probability theory. The multiple results of rolling a 6-sided die are a nice illustration of a discrete uniform distribution.
Discrete uniform distribution is likewise helpful in Monte Carlo reproduction. This is a demonstrating strategy that utilizations modified innovation to distinguish the probabilities of various results. Monte Carlo simulation is frequently used to estimate future events and identify dangers. There are also a number of data-producing and data analyzing functions linked with distributions that may be used to better understand the variables and their variation within a data collection. Probability density functions, cumulative density functions, and moment generating functions are examples of these functions.
A continuous uniform distribution (additionally alluded to as rectangular distribution) is factual dissemination with a limitless number of similarly reasonable quantifiable qualities. In contrast to discrete irregular factors, a ceaseless arbitrary variable can take any genuine worth inside a predetermined reach. A distribution is a basic graphical representation of a set of data. It can be displayed as a graph or a list, and it reveals which values of a random variable have a lower or greater probability of occurring.
There are a wide range of sorts of probability distributions, and the uniform dispersion is maybe the most straightforward of all. A nonstop uniform distribution as a rule arrives in a rectangular shape. An idealized random number generator is a nice example of a continuous uniform distribution. Every variable has an identical probability of occurring in a continuous uniform distribution, just as it does in a discrete uniform distribution.
However, there are an endless number of possible points. A uniform distribution is a probability distribution that states that the probabilities of different outcomes for a discrete collection of data are the same. A uniform distribution is anticipated to result in all conceivable outcomes having the same probability.
Information Sources: