Escape velocity is the speed that an object needs to be traveling to break free of a planet or moon’s gravity well and leave it without further propulsion. In physics, specifically, celestial mechanics, it is the minimum speed needed for a free, non-propelled object to escape from the gravitational influence of a massive body, that is, to eventually reach an infinite distance from it. For example, a spacecraft leaving the surface of Earth needs to be going 7 miles per second, or nearly 25,000 miles per hour to leave without falling back to the surface or falling into orbit.
Escape velocity is the speed at which an object must travel to break free of a planet or moon’s gravitational force and enter orbit. It is the minimum velocity that will allow a satellite to travel away from its planet and never return.
Escape velocity rises with the body’s mass and falls with the escaping object’s distance from its center. Since escape velocity depends on the mass of the planet or moon that a spacecraft is blasting off of, a spacecraft leaving the moon’s surface could go slower than one blasting off of the Earth, because the moon has less gravity than the Earth. A spacecraft leaving the surface of Earth, for example, needs to be going about 11 kilometers (7 miles) per second, or over 40,000 kilometers per hour (25,000 miles per hour), to enter orbit.
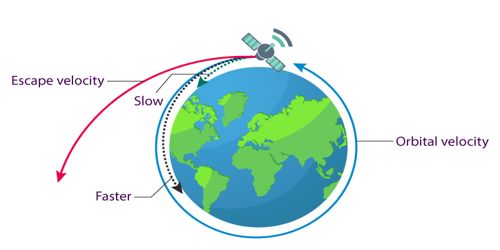
The escape velocity thus depends on how far the object has already traveled, and its calculation at a given distance takes into account the fact that without new acceleration it will slow down as it travels, due to the massive body’s gravity – but it will never quite slow to a stop. On the other hand, the escape velocity for Jupiter would be many times that of Earth’s because Jupiter is so huge and has so much gravity.
Escape velocity decreases with altitude and is equal to the square root of 2 (or about 1.414) times the velocity necessary to maintain a circular orbit at the same altitude. A rocket, continuously accelerated by its exhaust, can escape without ever reaching escape velocity since it continues to add kinetic energy from its engines. At the surface of the Earth, if atmospheric resistance could be disregarded, escape velocity would be about 11.2 km (6.96 miles) per second.
The velocity of escape from the less massive Moon is about 2.4 km per second at its surface. It can achieve escape at any speed, given sufficient propellant to provide new acceleration to the rocket to counter gravity’s deceleration and thus maintain its speed. A planet (or satellite) cannot long retain an atmosphere if the planet’s escape velocity is low enough to be near the average velocity of the gas molecules making up the atmosphere.
Information Source: