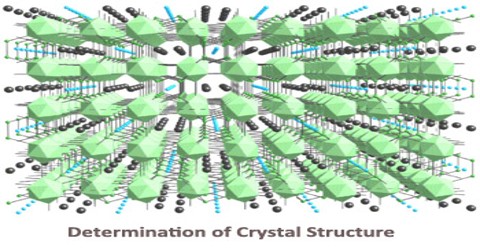
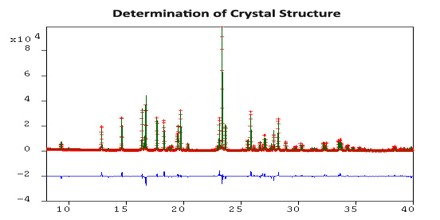
Determination of Crystal Structure
Crystalline Structure is any structure of ions, molecules, or atoms that are held together in an ordered, three-dimensional arrangement. Crystalline structure is one of two types of structural ordering of atoms, the other being the amorphous structure. The key difference in the crystalline and amorphous structure is the ordering of the structure. Crystalline structure can be thought of as the highest level of order that can exist in a material, while an amorphous structure is irregular and lacks the repeating pattern of a crystal lattice.
The crystal structures of simple ionic solids have long been rationalized in terms of Pauling’s rules, first set out in 1929 by Linus Pauling, referred to by many since as the “father of the chemical bond”. Pauling also considered the nature of the interatomic forces in metals, and concluded that about half of the five d-orbitals in the transition metals are involved in bonding, with the remaining nonbonding d-orbitals being responsible for the magnetic properties.
The crystal structure can be thought of as a small box with atoms, molecules, or ions located in specific areas of the box. The atoms within this box represent the smallest group of repeating atoms in the entire molecule. That means each atom found in the small box continues to repeat on and on in the same connectivity throughout the entire compound. The general arrangement and order of the atoms in the structure are directly related to the natural properties of the crystal. The crystalline structure is unique and specific for each material. That is to say, there will be no other compound organized in exactly the same way as any other. Essentially, the crystalline structure is the ‘identification marker’ for the compound.
The crystal structure and symmetry play a critical role in determining many physical properties, such as cleavage, electronic band structure, and optical transparency.
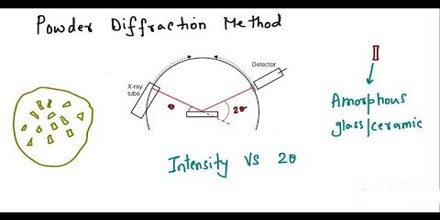
The ideal method for solving crystal structures is single-crystal X-ray diffraction. However, attempts to grow quality crystals for single-crystal analysis can prove difficult. Often these crystallization experiments produce powders that are analyzed using X-ray powder diffraction. Subsequently, the ability to determine the crystal structure from powder data is highly desirable.
Crystal Structure Determination from Powder Data
Given an indexable high-quality powder pattern, and the molecular fragments comprising the asymmetric unit, Powder Solve employs a three-step method for structure solution: (1) indexing the powder pattern; (2) refining the cell parameters, background coefficients, and peak intensities; and (3) solving the crystal structure.
The first step involves indexing the powder pattern to determine the cell parameters and crystal lattice class. Typically the most challenging step, it is important that the experimental powder pattern represents a single phase, displays little to no preferred orientation, and contains narrow peaks that have little overlap with neighboring peaks.
The second step involves a new technique called Powder Fit, a modified Pawley procedure to optimize cell parameters, peak profiles, integrated Bragg intensities, and background coefficients. These parameters are refined in order to minimize the weighted R-factor, Rwp, used to measure the similarity between the simulated and experimental powder patterns. The lower the Rwp value, the better the agreement.
The third step is Powder Solve itself. Before starting this step, the user must define the contents of the asymmetric unit as a series of non-overlapping rigid bodies where the junction of two rigid bodies defines a flexible torsion. Powder Solve then combines a Monte Carlo simulated annealing procedure with rigid-body Rietveld refinement with respect to all degrees of freedom in the system (i.e. torsional, translational, and rotational.) During each Monte Carlo step, the powder pattern is simulated and its agreement to the experimental powder data is calculated using Rwp. Subsequent structures are generated by changing one of the degrees of freedom in order to optimize the agreement between the powder patterns. For a problem with 10 degrees of freedom, the simulation typically takes 300,000 Monte Carlo steps.
Prediction of Crystal Structure
The difficulty of predicting stable crystal structures based on the knowledge of only the chemical composition has long been a stumbling block on the way to fully computational materials design. Now, with more powerful algorithms and high-performance computing, structures of medium complexity can be predicted using such approaches as evolutionary algorithms, random sampling, or metadynamics.
In the resonating valence bond theory, the factors that determine the choice of one from among alternative crystal structures of a metal or intermetallic compound revolve around the energy of resonance of bonds among interatomic positions. It is clear that some modes of resonance would make larger contributions be more mechanically stable than others, and that in particular a simple ratio of number of bonds to number of positions would be exceptional. The resulting principle is that a special stability is associated with the simplest ratios or “bond numbers”: 1⁄2, 1⁄3, 2⁄3, 1⁄4, 3⁄4, etc. The choice of structure and the value of the axial ratio, which determines the relative bond lengths, are thus a result of the effort of an atom to use its valency in the formation of stable bonds with simple fractional bond numbers.
Examples of Crystalline Structure
The crystalline structure of carbon is an age-old example and illustration of how the arrangement of atoms defines the properties of a crystal. Carbon may exist in one of three forms, and each form is significantly different due to its crystal structure. For instance, diamond and the lead used in a pencil are two completely different types of carbon.