The Navier-Stokes equations have long been used to mimic and describe the motion of fluids in nature, such as the flow of water in our oceans, the development of tornadoes in our atmosphere, and the flux of air around airplanes.
Yet, these equations are not fully understood by mathematicians. Although they are a useful tool for fluid flow prediction, we are yet unsure of their accuracy in describing fluids in all conceivable conditions.
The Navier-Stokes equations are one of the seven Millennium Problems, which are the seven most important unresolved problems in all of mathematics, according to the Clay Mathematics Institute of New Hampshire.
The Navier-Stokes Equation Millennium Problem challenges mathematicians to demonstrate that the Navier-Stokes equations always have “smooth” solutions.
Simply put, smoothness is the question of whether equations of this kind operate in a consistent and predictable manner. Consider a scenario in which a car’s gas pedal is depressed, causing the vehicle to speed to 10 mph, 20 mph, 30 mph, and finally 40 mph.
Yet, you might think there was a problem with the simulation if the gas pedal was depressed and the car quickly accelerated to 50 mph, 60 mph, and an endless amount of miles per hour.
This is what mathematicians hope to determine for the Navier–Stokes equations. Do they always simulate fluids in a way that makes sense, or are there some situations in which they break down?
This breakthrough is a testament to Dr. Hou’s tenacity in addressing the Euler problem and the intellectual environment that Caltech nutures. Caltech empowers researchers to apply sustained creative effort on complex problems even over decades to achieve extraordinary results.
Harry A. Atwater
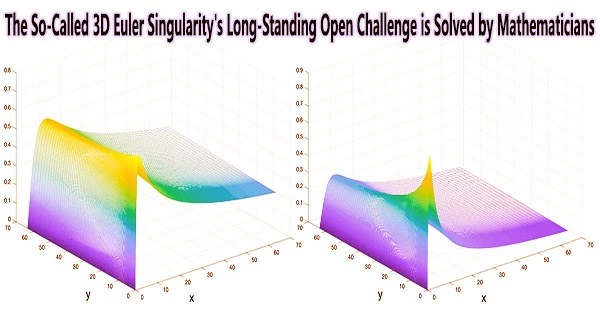
In a paper published on the preprint server arXiv, Caltech’s Thomas Hou, the Charles Lee Powell Professor of Applied and Computational Mathematics, and Jiajie Chen (Ph.D. ’22) of New York University’s Courant Institute, provide a proof that resolves a longstanding open problem for the so-called 3D Euler singularity.
The Navier-Stokes equations are simplified in the 3D Euler equation, and a singularity is the point at which an equation begins to collapse or “blow up,” which means it might abruptly and unpredictably turn chaotic (like the simulated car accelerating to an infinite number of miles per hour).
The proof is based on a scenario first proposed by Hou and his former postdoc, Guo Luo, in 2014.
Hou’s computation with Luo in 2014 discovered a new scenario that showed the first convincing numerical evidence for a 3D Euler blowup, whereas previous attempts to discover a 3D Euler blowup were either inconclusive or not reproduceable.
In the latest paper, Hou and Chen show definitive and irrefutable proof of Hou and Luo’s work involving 3D Euler equation blowup.
“It starts from something that behaves nicely, but then somehow evolves in a way where it becomes catastrophic,” Hou says.
“For the first ten years of my work, I believed there was no Euler blowup,” says Hou. After more than a decade of research since, Hou has not only proved his former self wrong, he’s settled a centuries-old mathematics mystery.
“This breakthrough is a testament to Dr. Hou’s tenacity in addressing the Euler problem and the intellectual environment that Caltech nutures,” says Harry A. Atwater, Otis Booth Leadership Chair of the Division of Engineering and Applied Science, Howard Hughes Professor of Applied Physics and Materials Science, and director of the Liquid Sunlight Alliance. “Caltech empowers researchers to apply sustained creative effort on complex problems even over decades to achieve extraordinary results.”
In addition to being a significant accomplishment in and of itself, Hou and colleagues’ joint work in demonstrating the presence of blowup with the 3D Euler equation also marks a significant advancement in the Navier-Stokes Millennium Problem. It would indicate a problem with one of the most fundamental equations used to describe nature if the Navier-Stokes equations could also explode.
“The whole framework that we set up for this analysis would be tremendously helpful for Navier-Stokes,” Hou says. “I have recently identified a promising blowup candidate for Navier-Stokes. We just need to find the right formulation to prove the blowup of the Navier-Stokes.”