Probability is essentially a measure of the possibility of something happening. And the likelihood ranges from 0 (impossible) to 1 (possible) (certain). In a sample space, the total of all probability for all events is 1. The likelihood of an event occurring if another event has already occurred is known as conditional probability. One of the most fundamental notions in probability theory is the concept of probability distributions.
Conditional probability is determined by increasing the probability of the former occasion by the refreshed probability of the succeeding, or contingent, occasion. Note that this probability doesn’t express that there is consistently a causal connection between the two occasions, just as it doesn’t show that the two occasions happen at the same time. This probability is denoted by the notation P(B|A), which denotes the likelihood of B given A. The Bayes’ theorem, which is one of the most prominent theories in statistics, is central to the idea of conditional probability.
P(A|B) could or might not be the same as P(A) (the unconditional probability of A). If P(A|B) = P(A), then occurrences A and B are said to be independent, meaning that knowing about one does not change the likelihood of the other. As such, conditional probability is the probability that an occasion has happened, considering some extra data about the results of an analysis.
The terms conditional probability and unconditional probability are often used interchangeably. Unconditional probability refers to the chance that an event will occur regardless of whether or not previous events have occurred or other circumstances exist. If the occurrences A and B are not independent, the probability of their interaction (the likelihood of both events occurring) is given by:
P(A and B) = P(A) P(B|A),
On the other hand, it can be written as;
P(A⋂ B) = P(A)P(B|A),
And, from this definition, the conditional probability P(B|A) can be defined as:
P(B|A) = P(A and B)|P(A)
Or, simply;
P(B|A) = P(A⋂ B)P(A), as long as P(A)> 0
While conditional probabilities can be incredibly beneficial, they are frequently used with minimal information. As a result, Bayes’ theorem may be used to reverse or convert a conditional probability. Furthermore, in certain circumstances, events A and B are independent occurrences, i.e., event A has no influence on the likelihood of event B; in these cases, the conditional probability of event B given event A, P(B|A), is basically the probability of event B, P(B). The Bayes’ theorem can be expressed mathematically as follows:
P(B|A) = P(B|A)P(A) / P(B)
Finally, a tree diagram may be used to find conditional probabilities. The probabilities in each branch of the tree diagram are conditional.
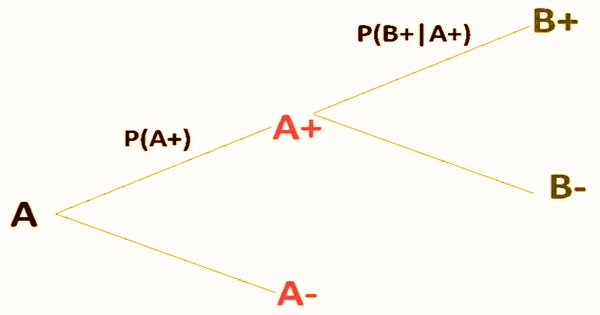
The Bayes theorem, commonly known as Bayes’ Rule or Bayes’ Law, is the cornerstone of Bayesian statistics. This collection of probability principles allows one to alter their forecasts of future occurrences based on new knowledge, resulting in more accurate and dynamic estimations. Mutually exclusive occurrences are events that cannot happen at the same time in probability theory.
All in all, on the off chance that one occasion has effectively happened, another can occasion can’t happen. Accordingly, the restrictive likelihood of fundamentally unrelated occasions is consistently zero. The law of absolute likelihood is just the utilization of the augmentation rule to quantify the probabilities in additional fascinating cases. Conditional probability, on the other hand, does not express the chance relationship between two occurrences, nor does it say that both events occur at the same time.
In domains as disparate as mathematics, insurance, and politics, conditional probability is applied. For example, a president’s re-election is determined by voter preferences, television advertising performance, and the likelihood that the opponent would make gaffes during debates.
Information Solution: