A bernoulli distribution is a discrete distribution of probability for a random experiment that has only two effects (usually called a “success” or a “failure”) in a Bernouilli study. The Bernoulli distribution, named after Jacob Bernoulli, a Swiss mathematician, is a discrete probability distribution of a random variable that takes 1 with probability p and 0 with probability q = 1 – p. In other words, it is a single-trial binomial distribution (e.g. a single coin toss). The chance of having a head (“success”) when flipping a coin, for example, is 0.5. The probability of “failure” is 1 – P (1 minus the probability of success, which for a coin toss also equals 0.5). The binomial distribution for n = 1 is a special case of this.
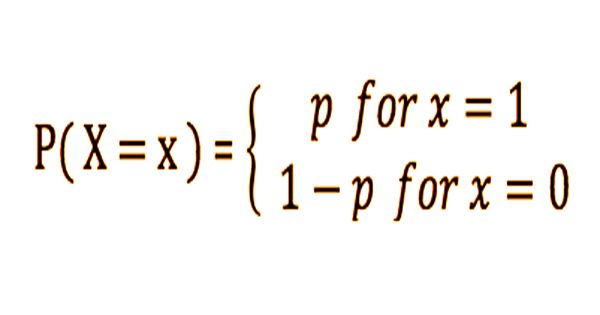
Example of Bernoulli Distribution
The Bernoulli distribution is a special case of a binomial distribution in which a single test is performed (for such a binomial distribution, n will be 1). The two-point distribution is also a special case, for which the potential outcomes need not be 0 and 1. However, the likelihood of success or failure for any Bernoulli trial does not have to be 50 percent. Imagine that in a bag we put 5 blue balls and 1 red ball and then drew one out randomly. As there are only two potential results, this is also a Bernoulli trial: either the ball is blue or it is red.
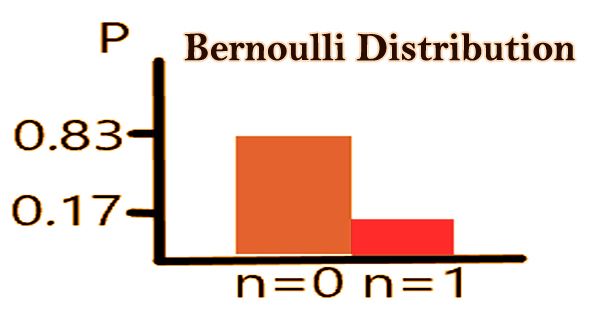
A significant part of any Bernoulli trial is that it is appropriate to be independent of each action. Which ensures that in the proceedings, the odds must remain the same; each case must be entirely different and have nothing to do with the previous event. A special case of the binomial distribution with n = 1 is the Bernoulli distribution. In the Bernoulli distribution, the two potential outcomes are labeled by n = 0 and n = 1 in which n = 1 (success) occurs with probability p and n = 0 (failure) occurs with probability 1 – p, and since a probability value is 0 < = p < = 1.
If an experiment has only two possible effects, “success” and “failure”, and if p is the likelihood of success, then “success” and “failure”, –
P(n) = pn (1 – p)1 – n
The Bernoulli distribution is often used in research and clinical trials to model a single person experiencing an occurrence such as death, a disease, or exposure to illness. The model is an outstanding predictor of the likelihood of an entity experiencing the event in question.
1 = “event” (P = p)
0 = “non event” (P = 1 – p)
To model disease incidence, Bernoulli distributions are used in logistic regression. A single toss of a biased/unbiased coin can be a simple example. The value of p will be 0.5 in the event of flipping an impartial or equal coin, giving a 50 percent chance of each outcome. However, in the case of a skewed coin flip where the probability of heads (success) is 0.6 while the probability of tails (failure) is 0.4, we must note that the probabilities of success and failure need not be equal all the time, like the distribution of Bernoulli.
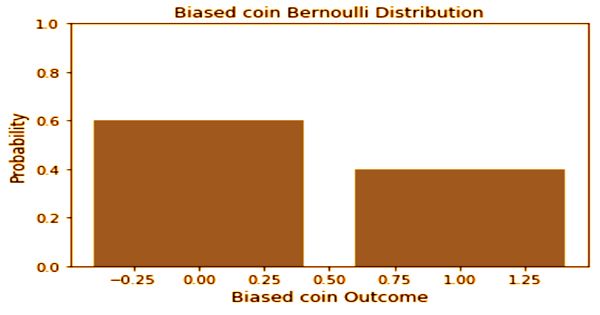
The probability of success (1) on the right is 0.4 in the above Bernoulli distribution, and the likelihood of failure (0) on the left is 0.6. If X1, … ,Xn are independent, identically distributed (i.i.d.) random variables, then their sum is distributed according to the binomial distribution of n and p parameters in all Bernoulli trials with success probability p. The distribution of the Bernoulli is simply B (1,p), also written as Bernoulli (p).
Information Sources: