There are several models that have been proposed to describe the collective movement of bacteria, also known as bacterial swarm behavior. One such model is the Vicsek model, which describes the motion of self-propelled particles that interact with one another through the alignment of their velocities. The model assumes that the velocity of each particle is influenced by the average velocity of the other particles in its neighborhood. This results in the formation of large-scale patterns of motion, such as vortices and lanes, that are observed in experiments with bacterial colonies.
Another model for collective bacterial movement is the self-propelled Voronoi model, which describes the motion of bacteria that move toward the regions of the highest chemical concentration, such as nutrients. The motion of each bacterium is determined by the locations of the other bacteria in its vicinity, and this leads to the formation of patterns such as waves and clustering.
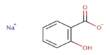
A new paper describes a mathematical model for bacterial motion that includes cell division and death, which are essential components of the cell cycle. Microorganisms, such as certain types of bacteria, form biofilms when they adhere to the surface of objects in a moist environment and begin to reproduce, resulting in the excretion of a slimy glue-like substance.
Our new model belongs to a class of models for ‘active matter’ that currently encounter a lot of interest in statistical physics. This field studies the collective properties of particle systems that have their own energy source – bacteria are an exemplary case.
Davide Breoni
These biofilms aren’t just unpleasant and unappealing however, they can be seriously troublesome. For example, in the medical field, the formation of biofilm can reduce the effectiveness of antibiotic treatments. The key to understanding biomass formation lies in understanding how bacteria behave en masse.
A new paper in EPJE by Heinrich-Heine-Universität, Düsseldorf, Germany, researcher Davide Breoni and his co-authors presents a mathematical model for the motion of bacteria that includes cell division and death, the basic ingredients of the cell cycle.
The team developed a mathematical model of bacterial movement in the process creating a link between statistical physics and biophysics. “Our new model belongs to a class of models for ‘active matter’ that currently encounter a lot of interest in statistical physics,” Breoni says. “This field studies the collective properties of particle systems that have their own energy source – bacteria are an exemplary case.”
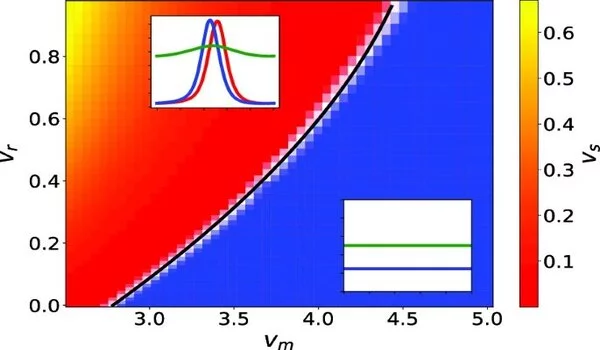
The model devised by the team delivered a surprise by suggesting that when it comes to movement bacteria can act as a unit.
“In the course of our investigation, we found out that the model predicts that the formation of bacterial colonies can occur through the build-up of traveling waves, concentrated ‘packages’ of bacteria,” Breoni adds. “We did not expect this to arise from such a simple model as ours.”
He believes that the results should be interesting to the general public who may be aware of bacterial colonies, but not know how they move in a collective way.
Breoni concludes by pointing out this is a very simple model suggesting how the research could proceed from here. “We could try to make the model more realistic and confront the results to experiment to test its predictions,” he says. “On the other hand, this research is very much curiosity-driven and results from intense discussions among the researchers – an approach we’d like to maintain so we can continue to surprise ourselves with our findings.”
Recent models combine the two above approaches, that consider both nutrient-attraction and alignment interaction. In these models, the bacteria movement, instead of being based on the purely random walk or a gradient following, is a combination of both. It’s important to keep in mind that bacterial swarming is a complex phenomena, and many factors, including nutrient availability, bacteria density, and species-specific characteristics can all contribute to the final behavior of the swarm.