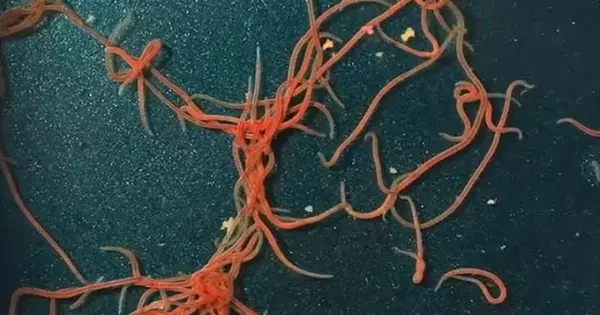
Wiggly worm knots are fascinating mathematical objects that have been studied in knot theory. They are also known as unknots or wild knots. Knot theory is a mathematical branch that studies the mathematical properties and classification of knots. A knot is a closed curve embedded in three-dimensional space that can be continuously deformed into a simple, untwisted loop with no self-intersections. In other words, by moving the knot in space smoothly, an unknot can be transformed into a circle.
Researchers wanted to know how blackworms perform tangling and ultrafast untangling movements for a variety of biological functions. They investigated the tangles’ topology. Their research could inform the design of fiber-like, shapeshifting robotics that self-assemble and move in ways that are fast and reversible.
For millennia, humans have used knots for a variety of purposes, such as tying rope, braiding hair, and weaving fabrics. However, there are organisms that are far superior — and much faster — at tying knots and untangling them.
Capturing the inside structure of a live worm blob was a real challenge. We tried X-rays, confocal microscopy, and tomography for months, but none of them provided us with the real-time resolution we required. Finally, ultrasound proved to be the solution.
Harry Tuazon
Thousands of tiny California blackworms intricately tangle themselves to form ball-shaped blobs that allow them to perform a variety of biological functions. Most impressively, while the worms tangle for several minutes, they can untangle in milliseconds, allowing them to flee at the first sign of a predator threat.
Saad Bhamla, an assistant professor in Georgia Tech’s School of Chemical and Biomolecular Engineering, wanted to know how blackworms perform their tangling and untangling movements. Bhamla and a team of Georgia Tech researchers collaborated with MIT mathematicians to conduct the investigation. Their findings, published in Science, could have an impact on the design of fiber-like, shapeshifting robotics that self-assemble and move in quick and reversible ways. The study also demonstrates how cross-disciplinary collaboration can provide answers to some of the most perplexing questions in various fields.

Capturing the Inside of a Worm Blob
Bhamla and Harry Tuazon, a graduate student in Bhamla’s lab, have been studying California blackworms for years, observing how they use collective movement to form blobs and then disperse, fascinated by the science of ultrafast movement and collective behavior.
“We wanted to understand the exact mechanics behind how the worms change their movement dynamics to achieve tangling and ultrafast untangling,” explained Bhamla. “Also, these are not just typical filaments like string, ethernet cables, or spaghetti — these are living, active tangles that are out of equilibrium, which adds a fascinating layer to the question.”
Tuazon, a co-first author of the study, collected videos of his experiments with the worms, including macro videos of the worms’ collective dispersal mechanism and microscopic videos of one, two, three, and several worms to capture their movements.
“I was shocked when I pointed a UV light toward the worm blobs and they dispersed so explosively,” Tuazon said. “But to understand this complex and mesmerizing maneuver, I started conducting experiments with only a few worms.”
Bhamla and Tuazon approached MIT mathematicians Jörn Dunkel and Vishal Patil (at the time a graduate student and now a postdoctoral fellow at Stanford University) about working together. Tuazon’s videos piqued the interest of the two theorists, who specialize in knots and topology.
“Knots and tangles are a fascinating area where physics and mechanics meet some very interesting math,” said Patil, the paper’s co-first author. “These worms seemed like a good playground for investigating topological principles in filament-based systems.”
A key moment for Patil was when he viewed Tuazon’s video of a single worm that had been provoked into the escape response. Patil noticed the worm moved in a figure-eight pattern, turning its head in clockwise and counterclockwise spirals as its body followed.
The researchers thought this helical gait pattern might play a role in the worms’ ability to tangle and untangle. But to mathematically quantify the worm tangle structures and model how they braid around each other, Patil and Dunkel needed experimental data.
Bhamla and Tuazon set out to develop an imaging technique that would allow them to look inside the worm blob and collect more data. They arrived at an unexpected solution after much trial and error: ultrasound. They were finally able to see inside the intricate worm tangles by immersing a live worm blob in nontoxic jelly and using a commercial ultrasound machine.
“Capturing the inside structure of a live worm blob was a real challenge,” Tuazon admitted. “We tried X-rays, confocal microscopy, and tomography for months, but none of them provided us with the real-time resolution we required. Finally, ultrasound proved to be the solution.”
Explaining Tangling and Untangling
To answer the question of how the worms untangle quickly, a combination of mechanics and topology was required. Patil created a mathematical model to demonstrate how helical gaits can cause tangling and untangling. Patil was able to create a visualization of worms tangling by testing the model with a simulation framework.
The model predicted that each worm would entangle itself with at least two other worms, explaining why the worm blobs were so cohesive. Patil then demonstrated that the same helical gaits could explain how they untangle. The simulations were startlingly similar to real ultrasound images, demonstrating that the worms’ alternating helical wave motions enabled the tangling and ultrafast untangling escape mechanisms.
“What’s striking is how complicated these tangled structures are. They are disordered and complex structures, but these living worm structures can manipulate these knots to perform critical functions,” Patil explained.
While the worms’ helical gait has been known for decades, no one had ever made the connection between that movement and how they escape. The researchers’ work revealed how individual worms’ mechanical movements influence their emergent collective behavior and topological dynamics. It also has the distinction of being the first mathematical theory of active tangling and untangling.
“This may appear to be a trivial observation, but its implications are far-reaching. Active filaments are found everywhere in biological structures, from DNA strands to entire organisms,” said Eva Kanso, program director at the National Science Foundation and a mechanical engineering professor at the University of Southern California.
“These filaments serve a variety of functions and can serve as a general motif for engineering multifunctional structures and materials with variable properties. Future bioinspired materials may defy the limits of conventional structures by exploiting the interplay between mechanics, geometry, and activity, just as worm blobs perform remarkable tangling and untangling feats.”