Theorems on Straight Lines and Plane
In mathematics, the term “line” actually refers to the “straight line”. It is a one-dimensional figure that extends in two opposite directions. A straight line can be defined as an interconnected set of an infinite number of points. The length of a line is infinite, while it has zero or no width as well as height.
A normal to the plane is drawn from the point where the line touches the plane. This normal forms an angle with the line. Then, the angle between the line and the plane is equivalent to the complement of the angle between the line and the normal.
Theorem: If a straight line is perpendicular to each of two intersecting straight lines at their point of intersection, it is also perpendicular to the plane in which they lie.
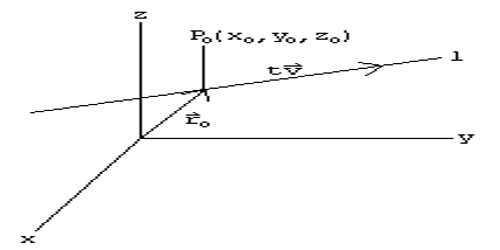
Let the straight line OP be perpendicular to each of two intersecting straight lines OM and ON at their point of intersection O and XY be the plane in which OM and ON lie. We are to prove that the straight line OP is perpendicular to the plane XY.
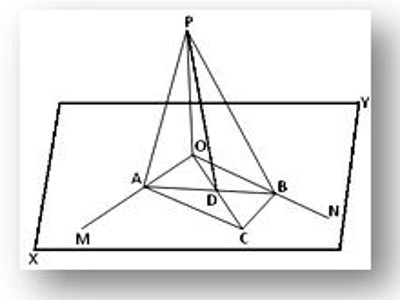
Construction: Through O draw any straight line OC in the XY plane and take any point C on it. Now, complete the parallelogram OACB in the XY plane by drawing lines CB and CA parallel to OM and ON respectively. Join AB, which cuts OC at D. Join PA, PB, and PD.
Proof: Since OACB is a parallelogram and its two diagonals AB and OC intersect at D, hence D is the mid-point of AB (Since diagonals of a parallelogram bisect each other).
Therefore, PD is a median of the triangle APB; hence, by Apollonius theorem we get,
AP² + BP² = 2 (AD² + PD²) . . . (1)
Again, OC is a median of the triangle OAB; hence, by the same theorem we get,
OA² + OB² = 2 (AD² + OD²) . . . (2)
Subtracting (2) from (1) we get,
(AP² – OA²) + (BP² – OB²) = 2 (PD² – OD²) . . . (3)
Now, OP is perpendicular to both OA and OB.
Therefore, AP² = OA² + OP²
or, AP² – OA² = OP² . . . (4)
and BP² = OB² + OP ²
or, BP ² – OB² = OP² . . . (5)
From (3), (4) and (5) we get,
OP² + OP² = 2 (PD² – OD²)
or, 2. OP ² = 2 (PD² – OD²)
or, OP ² = PD² – OD²
or, OP ² + OD² = PD²
Therefore, ∠POD (i.e., ∠POC) is a right angle.
Therefore, OP is perpendicular to OC at O. But OC is any straight line through O in the plane XY. Therefore, OP is perpendicular to the plane XY at O.
Information Source: