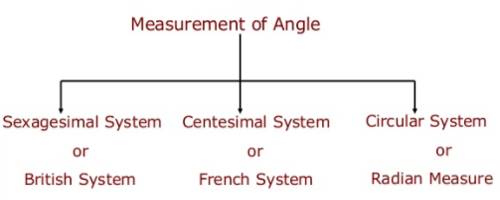
Sexagesimal, Centesimal and Circular Systems
We know, Sexagesimal, Centesimal and Circular Systems are the three different systems of measuring angles. Sexagesimal system is also known as English system and the centesimal system is known as French system.
There are three systems of measurement of angles:
(i) Sexagesimal or English system: when the right angle is divided into 90 equal parts called degree then we use a sexagesimal system.
(ii) Centesimal or French system: when the right angle is divided into 100 equal parts called grades then we use a Centesimal System system.
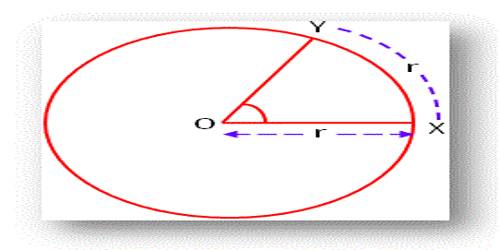
(iii) Circular system: In this system degrees are given in radian.1 radian is the measure of an angle subtended at the center of the circle by an arc length equal to the radius of the circle.
To convert the one system to the other system its very necessary to know the relation between the Sexagesimal system, Centesimal system, and Circular system.
The relation between Sexagesimal, Centesimal and Circular systems are discussed below:
Since 90° = 1 right angle, hence, 180° = 2 right angles.
Again, 100g = 1 right angle; hence, 200g = 2 right angles.
And, πc = 2 right angles.
Therefore, 180° = 200g = πc.
Let, D°, Gg and Rc be the sexagesimal, centesimal and circular measures respectively of a given angle.
Now, 90° = 1 right angle
Therefore, 1° = 1/90 right angle
Therefore, D° = D/90 right angle
Again, 100g = 1 right angle
Therefore, 1g = 1/100 right angle
Therefore, Gg = G/100 right angle.
And, 1c = 2/π right angle
Therefore, Rc = 2R/π right angle.
Therefore we have,
D/90 = G/100 = 2R/π
or,
D/180 = G/200 = R/π
- The circular measure of an angle is π/8; find its value in sexagesimal and centesimal systems.
Solution:
πc/8
= 180°/8, [Since, πc = 180°)
= 22°30′
Again, πc/8
= 200/8 [Since, πc = 200g) = 25g
Therefore, the sexagesimal and centesimal measures of the angle πc/8 are 22°30′ and 25g respectively.
- Find in sexagesimal, centesimal and circular units an internal angle of a regular Hexagon.
Solution:
We know that the sum of the internal angles of a polygon of n sides = (2n – 4) rt. angles.
Therefore, the sum of the six internal angles of a regular pentagon = (2 × 6 – 4) = 8 rt. angles.
Hence, each internal angle of the Hexagon = 8/6 rt. angles. = 4/3 rt. angles.
Therefore, each internal angle of the regular Hexagon in sexagesimal system measures 4/3 × 90°, (Since, 1 rt. angle = 90°) = 120°;
In centesimal system measures
4/3 × 100g (Since, 1 rt. angle = 100g)
= (400/3)g
= 133 x 1/3
and in circular system measures (4/3 × π/2)c, (Since, 1 rt. angle = πc/2)
= (2π/3)c.
Information Source: