Converse of the theorem on parallel lines and plane:
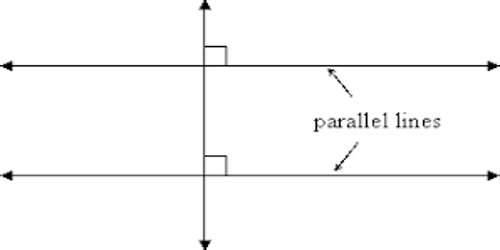
Theorem: If two straight lines are parallel and if one of them is perpendicular to a plane, then the other is also perpendicular to the same plane. When lines and planes are perpendicular and parallel, they have some interesting properties.
Lines and planes are parallel to one another as in the ordinary geometry: two lines when they lie in one plane and do not intersect, a line and a plane or two planes when they lie in one hyperplane and do not intersect.
Let PQ and RS be two parallel straight lines of which PQ is perpendicular to the plane XY. We are to prove that the straight line RS is also perpendicular to the plane XY.
If two straight line are both perpendicular to a plane then they are parallel.
Let two straight lines PQ and RS be both perpendiculars to the plane XY. We are to prove that the lines PQ and RS are parallel.
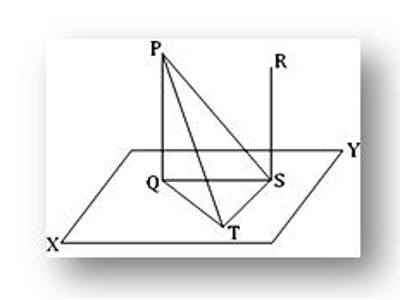
Following the same construction as in theorem on parallel lines and plane, it can be proved that ST is perpendicular to PS. Since, RS is perpendicular to the plane XY, hence RS is perpendicular to TS, a line through S in the plane XY i.e., TS is perpendicular to RS. Again, by construction, TS is perpendicular QS. Therefore, TS is perpendicular to each of the straight lines QS, PS and RS at S. hence, QS, PS, and RS are co-planar (by theorem on co-planar). Again, PQ, QS, and PS are co-planar (Since they lie in the plane of the triangle PQS). Thus, PQ and RS both lie in the plane of PS and QS i.e., PQ and RS are co-planar.
Again, by hypothesis,
∠PQS = 1 right angle and ∠RSQ = 1 right angle.
Therefore, ∠PQS + ∠RSQ = 1 right angle + 1 right angle = 2 right angles.
Therefore, PQ is parallel to RS.
Information Source: