Place Values – Expanded Form
Bundling objects into sets of 10 (then 10 tens into one hundred, and 10 hundreds into one thousand, etc.) is the basis of our place value system. The power of the place value system is that it makes counting and operating on numbers much simpler than working with individual objects.
Key Concepts:
- When adding two-digit numbers, we add tens with tens and ones with ones (sometimes composing a ten).
- We can find ten more or ten less without having to count.
- We can use our understanding of place value to add and subtract ten to/from multiples of ten.
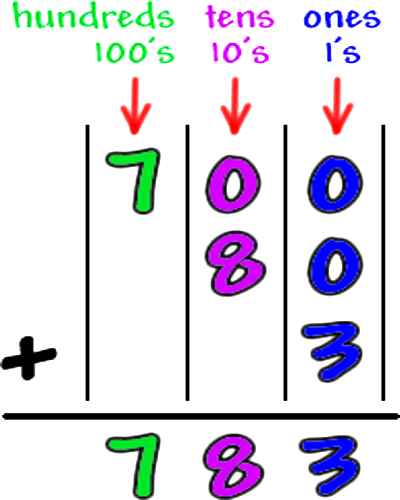
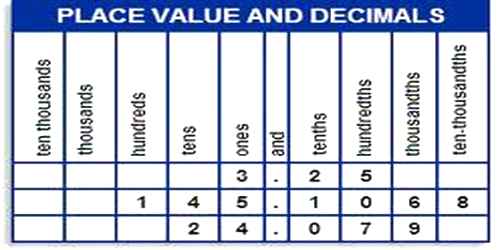
In our decimal number system, the value of a digit depends on its place, or position, in the number. Each place has a value of 10 times the place to its right.
Example:
Numbers, such as 784, have three digits. Each digit is a different place value.
The first digit is called the hundreds’ place. It tells you how many sets of one hundred are in the number. The number 784 had seven hundreds.
The middle digit is the tens’ place. It tells you that there are 8 tens in addition to the seven hundreds.
The last or right digit is the ones’ place which is 4 in this example. Therefore, there are 7 sets of 100, plus 8 sets of 10, plus 4 ones in the number 784.

Information Source: