Physicists and computer scientists have lately expanded on the contemporary theory of computational thermodynamics. The researchers combine methodologies from statistical physics and computer science to present mathematical equations that indicate the minimum and maximum expected energy cost of computational operations based on randomness, which is a strong tool in current computers.
Every computing system, biological or manmade, from cells to brains to laptops, has a price. This is not the price, which is obvious, but rather an energy cost related to the work necessary to run a program and the heat dissipated in the process.
Researchers at SFI and elsewhere have spent decades developing a thermodynamic theory of computation, but previous work on the energy cost has focused on basic symbolic computations, such as erasing a single bit, that are difficult to apply to less predictable, real-world computing scenarios.
In a study published in Physical Review X, four physicists and computer scientists elaborate on the contemporary idea of computation thermodynamics. The researchers combine methodologies from statistical physics and computer science to present mathematical equations that indicate the minimum and maximum expected energy cost of computational operations based on randomness, which is a strong tool in current computers.
Many computational machines, when viewed as dynamical systems, have this property where if you jump from one state to another you really can’t go back to the original state in just one step.
Gülce Kardes
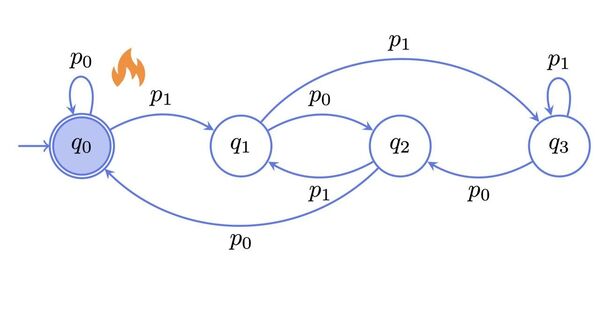
In particular, the framework offers insights into how to compute energy-cost bounds on computational processes with an unpredictable finish. For example: A coin-flipping simulator may be instructed to stop flipping once it achieves 10 heads. In biology, a cell may stop producing a protein once it elicits a certain reaction from another cell. The “stopping times” of these processes, or the time required to achieve the goal for the first time, can vary from trial to trial. The new framework offers a straightforward way to calculate the lower bounds on the energy cost of those situations.
The research was conducted by SFI Professor David Wolpert, Gonzalo Manzano (Institute for Cross-Disciplinary Physics and Complex Systems, Spain), Édgar Roldán (Institute for Theoretical Physics, Italy), and SFI graduate fellow Gülce Kardes (CU Boulder). The study uncovers a way to lower-bound the energetic costs of arbitrary computational processes. For example: an algorithm that searches for a person’s first or last name in a database might stop running if it finds either, but we don’t know which one it found. “Many computational machines, when viewed as dynamical systems, have this property where if you jump from one state to another you really can’t go back to the original state in just one step,” says Kardes.
Around a decade ago, Wolpert began looking into how to apply ideas from nonequilibrium statistical physics to computation theory. He describes computers as an out-of-equilibrium system, and stochastic thermodynamics provides physicists with a method for studying nonequilibrium systems. “If you put those two together, it seemed like all kinds of fireworks would come out, in an SFI kind of spirit,” according to him.
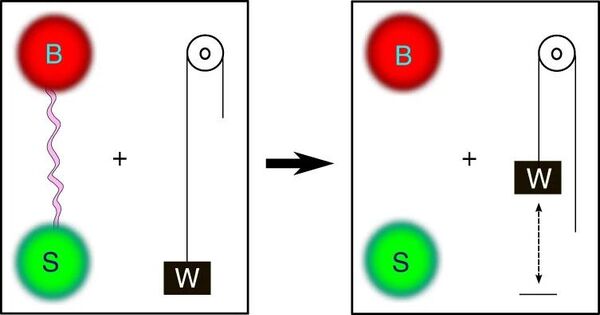
In recent works that provided the framework for this new paper, Wolpert and colleagues proposed the concept of a “mismatch cost,” or a measure of how much the cost of a computation exceeds Landauer’s bound. Rolf Landauer, a physicist, proposed this limit in 1961 to specify the minimal amount of heat required to modify information in a computer. Knowing the mismatch cost, Wolpert says, could inform strategies for reducing the overall energy cost of a system.
Across the Atlantic, co-authors Manzano and Roldán have been developing a tool from the mathematics of finance — the martingale theory — to address the thermodynamic behavior of small fluctuating systems at stopping times. Roldán et. al.’s “Martingales for Physicists” helped pave the way to successful applications of such a martingale approach in thermodynamics.
Wolpert, Kardes, Roldán, and Manzano extend these tools from stochastic thermodynamics to the calculation of a mismatch cost to common computational problems in their PRX paper.
Taken together, their research point to a new avenue for finding the lowest energy needed for computation in any system, no matter how it’s implemented. “It’s exposing a vast new set of issues,” Wolpert says.
It could also have a very practical impact by pointing out new methods to make computing more energy efficient. According to the National Science Foundation, computers consume between 5% and 9% of global generated electricity, but if current growth rates continue, this figure might rise to 20% by 2030. However, earlier work by SFI researchers reveals that modern computers are extremely inefficient: biological systems, on the other hand, are around 100,000 times more energy-efficient than human-built computers. According to Wolpert, one of the key incentives for developing a broad thermodynamic theory of computation is to discover innovative techniques to lower the energy consumption of real-world devices.