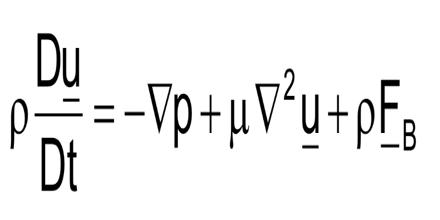Navier-Stokes Equations are time-dependent and consist of a continuity equation for conservation of mass, three conservation of momentum equations and a conservation of energy equation. Navier–Stokes Equations represent the conservation of momentum, while the continuity equation represents the conservation of mass. These equations are at the heart of fluid flow modeling. This equations are a set of nonlinear partial differential equations that describe the flow of fluids. They are useful because they describe the physics of many phenomena of scientific and engineering interest. They may be used to model the weather, ocean currents, water flow in a pipe and air flow around a wing.
Navier–Stokes Equations