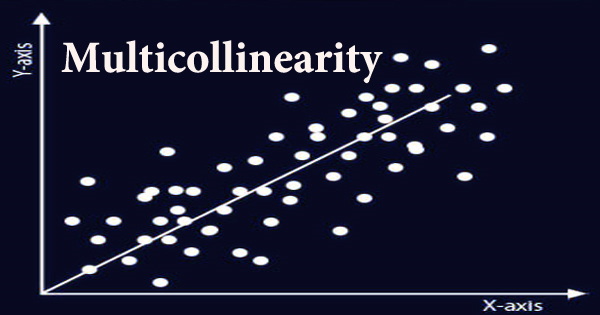
Multicollinearity (also known as collinearity) is a statistical phenomenon in which one predictor variable in a multiple regression model may be predicted linearly from the others with a high degree of accuracy. The variables are unrelated, although they do appear to be linked in some way. When a researcher or analyst tries to figure out how well each independent variable can be utilized to predict or explain the dependent variable in a statistical model, multicollinearity can lead to skewed or misleading conclusions.
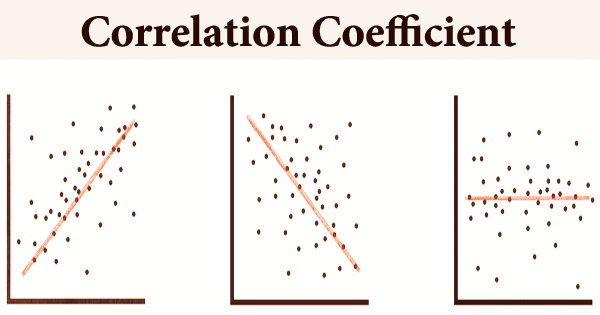
Calculating correlation coefficients for all pairs of predictor variables is a simple approach to discover multicollinearity. Perfect multicollinearity occurs when the correlation coefficient, r, is precisely +1 or -1. If feasible, one of the variables should be eliminated from the model if r is near to or precisely -1 or +1. It’s being studied in data science and business analytics schools, and it’s quickly becoming a crucial tool for making data-driven decisions. Multicollinearity is a type of data disturbance, and if it’s detected in a model, it might indicate that the entire model and its results aren’t trustworthy.
Multicollinearity, in general, can result in larger confidence intervals, resulting in less accurate probability when it comes to the influence of independent variables in a model. It has no effect on the model’s overall predictive power or reliability, at least within the sample data set; it simply impacts individual predictor computations. It has numerous flaws that can impact a model’s efficacy, and knowing why can lead to stronger models and improved decision-making abilities.
When creating multiple regression models with two or more variables, it is preferable to utilize independent variables that are not correlated or repetitive. Poorly planned studies, data that is 100% observational, or data collecting methods that cannot be altered can all lead to data-based multicollinearity. There is no mistake on the side of the researcher when variables are highly linked (typically owing to data collected from purely observational studies).
Multicollinearity is usually recognized to a certain degree of precision. The tolerance is generally computed using the variance inflation factor, and if it is 10 or above, the link between the two variables is deemed troublesome. A multivariate regression model with collinear predictors can show how well the whole bundle of predictors predicts the outcome variable, but it may not provide accurate information about any particular predictor or which predictors are redundant in relation to others.
In a multivariate regression model, multicollinearity shows that collinear independent variables are connected in some way, whether or not the relationship is causal. It can cause large fluctuations in a model’s independent variables, and it weakens the model’s coefficients. The model’s outputs may become null if the link between variables becomes difficult to comprehend. Multicollinearity, in any case, is a property of the data matrix, not the underlying statistical model.
Causes for multicollinearity can also include:
- Insufficient data. In some cases, collecting more data can resolve the issue.
- It’s possible that dummy variables are being utilized wrongly. For example, the researcher may overlook one category or include a fake variable for each one (e.g. spring, summer, autumn, winter).
- Incorporating a regression variable that is actually a mixture of two additional variables. Include “total investment income” when total investment income equals income from stocks and bonds plus income from savings interest, for example.
- Including two variables that are the same (or nearly identical). Weight in pounds vs. weight in kilograms, or investment income vs. savings/bond income, for example.
In a multivariate regression model, multicollinearity refers to when more than two explanatory variables are substantially linearly linked. In other words, when two independent variables are significantly linked, it can occur. It can also happen if an independent variable is calculated using data from other variables in the data set, or if two independent variables provide comparable and consistent findings.
If one or more precise linear connections exist among some of the variables, a collection of variables is completely multicollinear mathematically. When working with regression models or creating them from the ground up, it’s important to be aware of the hazards that might distort the data and reduce their dependability. One of the most popular methods for overcoming multicollinearity is to first identify collinear independent variables and then eliminate all except one.
Information Sources: