Linear elasticity is a key topic in solid mechanics, specifically the study of materials’ mechanical behavior. It is a mathematical model that describes how solid things deform and become inwardly strained in response to specific loading circumstances. It describes the relationship between the stress applied to a material and the strain experienced by the material, assuming that the relationship is linear and obeys Hooke’s Law. It is a simplified version of the more comprehensive nonlinear theory of elasticity and a subfield of continuum mechanics.
The key “linearizing” assumptions of linear elasticity are minuscule strains or “small” deformations (or strains), as well as linear connections between stress and strain components. Furthermore, linear elasticity only applies to stress states that do not result in yielding.
These assumptions are reasonable for a variety of engineering materials and design contexts. Linear elasticity is so widely utilized in structural analysis and engineering design, frequently with the help of finite element analysis.
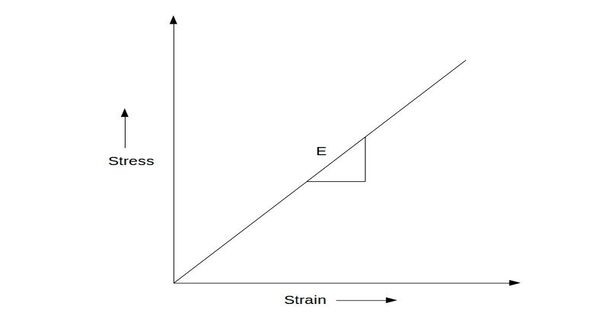
Hooke’s Law states that the stress (𝜎) applied to a material is directly proportional to the strain (𝜀) it experiences, with the proportionality constant being the material’s modulus of elasticity,
(𝐸): σ = Eε
In this equation:
- σ represents stress (force per unit area).
- ε represents strain (deformation per unit length).
- E represents the modulus of elasticity, also known as Young’s modulus. It quantifies the stiffness of the material and how much it deforms under stress.
Linear elasticity assumes that the stress-strain relationship holds true within the material’s elastic limit, which means that after the stress is released, the material returns to its original shape and does not incur irreversible deformation. Beyond the elastic limit, the material may display nonlinear behavior, including plastic deformation.
Linear elasticity theory is widely used in engineering and material science to examine the behavior of structures under load, design mechanical components, and anticipate how materials will respond to different conditions. It is the foundation for many analytical and numerical methods used in structural analysis and design.