Reducing redundant information in data sets and complex networks to find simplifying patterns is a scientific challenge in many knowledge fields. Furthermore, detecting the dimensionality of the data remains a difficult problem. An article published in the journal Nature Communications describes a method for inferring the dimensionality of complex networks using hyperbolic geometrics, which capture the complexity of relational structures in the real world across many domains.
Researchers M. ngeles Serrano and Marián Boguá from the Faculty of Physics and the UB Institute of Complex Systems (UBICS), as well as Pedro Almargo from the University of Sevilla’s Higher Technical School of Engineering, are among the study’s authors. The research study presents a multidimensional hyperbolic model of complex networks that reproduces connectivity with ultra-low and customizable dimensionality for each network. This allows for a more accurate characterization of its structure (for example, at the community level) and an improvement in its predictive capability.
The study uncovered unexpected patterns, such as the extremely low dimensions of molecular networks associated with biological tissues, the slightly higher dimensionality required by social networks and the Internet, and the discovery that brain connectomes are close to three dimensions in their automatic organization.
Our estimates of the dimensionality of complex networks are well below our estimates based on Euclidean space, since hyperbolic space is better suited to represent the hierarchical structure of real complex networks.
Professor Marián Boguñá
Hyperbolic versus Euclidean geometry
The inherent geometry of data sets or complex networks is not obvious, which makes determining the dimensionality of real networks difficult. Another challenge is that the definition of distance must be established based on their relational and connectivity structure, which necessitates the use of sophisticated models.
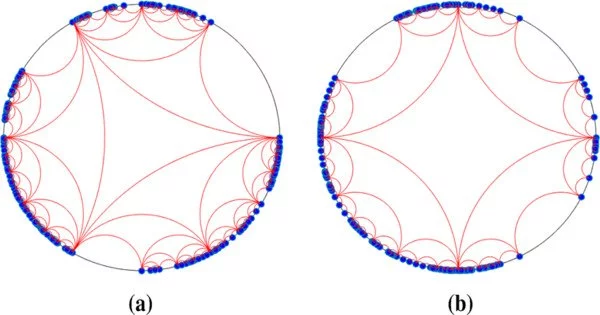
Now, the new approach is based on the geometry of complex networks, and more specifically, on the configurational geometric model or SD model. “This model, which we have developed in previous work, describes the structure of complex networks based on fundamental principles,” says the lecturer M. Ángeles, ICREA researcher at the Department of Condensed Matter Physics of the UB.
“More specifically – he continues, the model postulates a law of interconnection of the network elements (or nodes) that is gravitational, so nodes that are closer in a similarity space of spherical geometry in D dimensions and with more popularity – an extra dimension corresponding to the importance of the node are more likely to establish connections.”
The similarity and popularity variables are combined in the study to generate the model’s hyperbolic geometry, which emerges as the natural geometry representing the hierarchical architecture of complex networks.
Previously, the team used the S1 model, the simplest version of the one-dimensional SD model, to explain many common features of real-world networks, such as the small-world property (the six degrees of separation), heterogeneous distributions of the number of neighbors per node, and high levels of transitive relationships (triangle connections that can be illustrated with the expression my friend’s friend is also my friend).
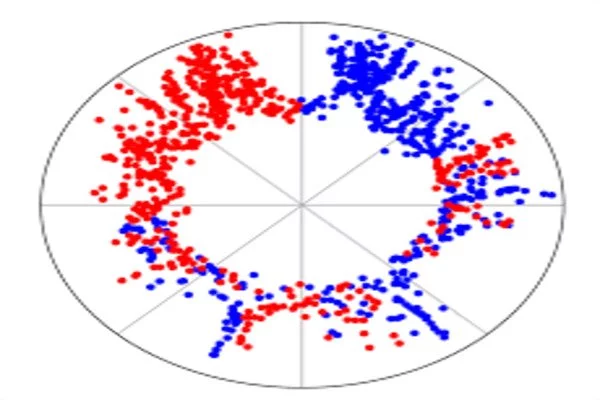
“In addition, the application of statistical inference techniques allows us to obtain real network maps in the hyperbolic plan that are congruent with the established model,” she says. “Beyond visualisation, these representations have been used in a multitude of tasks, including efficient navigation methods, the detection of self-similarity patterns, the detection of strongly interacting communities of nodes, and the implementation of a network renormalisation procedure that reveals hidden symmetries in the multi-scale organisation of complex networks and allows the production of network replicas at reduced or enlarged scales.”
Now, the team infers the dimensionality of the hyperbolic space underlying the real networks from properties that relate to the dimension of their geometry. In particular, the work measures the statistics of higher-order cycles (triangles, squares, pentagons) associated with the connections.
A methodology applicable to all complex networks
In computer science, the applied techniques are based on data that typically make definitions of similarity distance between their elements, an approach that involves the construction of graphs that are mapped onto a latent space of Euclidean features.
“Our estimates of the dimensionality of complex networks are well below our estimates based on Euclidean space, since hyperbolic space is better suited to represent the hierarchical structure of real complex networks. For example, the Internet only requires D = 7 dimensions to be mapped into the hyperbolic space of our model, whereas this name is multiplied by six and scales to D = 47 in one of the most recent techniques using Euclidean space,” says Professor Marián Boguñá.
In addition, techniques for mapping complex data usually assume a latent space, with a predetermined name of dimensions, or implement heuristic techniques to find a suitable value. Thus, the new method is based on a model that does not need the spatial mapping of the network to determine the dimension of its geometry.
In the field of network science, many methodologies use the shortest distances to study the connectivity structure of the network (shortest paths) as a metric space. However, these distances are strongly affected by the small-world property and do not provide a wide range of distance values.
“Our model uses a completely different definition of distance based on an underlying hyperbolic space, and we do not need to map the network. Our methodology is applicable to any real network or data series with complex structure and with a size that is typically thousands or tens of thousands of nodes but can reach hundreds of thousands in a reasonable computational time,” says M. Ángeles Serrano.
What is the real dimensionality of social networks and the Internet?
According to the study’s findings, social networks and the Internet rank higher (between 6 and 9) than networks in other domains. However, it is still very low – 6 to 7 times lower – when compared to other methods. This reflects the fact that interactions in these systems are more complex and influenced by a wider range of variables.
Friendship-based social networks, on the other hand, rank first in terms of dimensionality. “This is an unexpected result, because one might think that friendship is a more liberated type of affective relationship,” M. Ángeles Serrano says. “Our findings point to the fact that homophily in human interactions is determined by a variety of sociological factors such as age, gender, social class, beliefs, attitudes, or interests.”
Even though the Internet is a technological network, its greater dimensionality reflects the fact that, for an autonomous system, connecting does not simply mean accessing the system, as one might assume at first. On the contrary, many different factors influence the formation of these connections, and as a result, a variety of other relationships may exist.
“What is really surprising, both for social networks and the internet, is that our theoretical framework — which does not use any annotations about connections beyond their existence — is able to capture this multidimensional reality that is not explicit in our data,” concludes the team, which is currently working on creating hyperbolic multidimensional maps of complex networks that are congruent with the SD model’s theoretical framework.