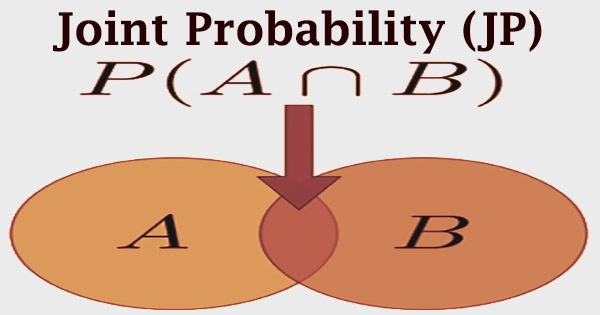
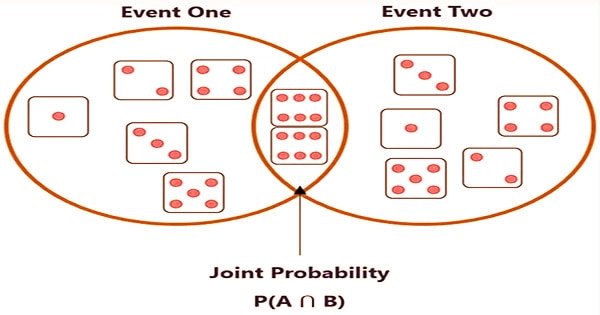
In probability theory, a joint probability is a chance that two occurrences will happen at the same time. It’s a statistical metric that assesses the chances of two occurrences occurring at the same time and in the same place. To put it another way, the joint probability is the probability that two occurrences will occur at the same moment. It’s the chance that event X will happen at the same time as event Y.
Probability is a field of mathematics that studies the probability of a random event occurring. In basic terms, it is the probability of a specific occurrence occurring. Joint probability can be expressed in a variety of ways. The chance of events intersecting is represented by the formula below:
P (X ⋂ Y)
where:
X, Y = Two different events that intersect
P (X and Y), P (XY) = The joint probability of X and Y
An intersection is a symbol “∩” in a joint probability. The point where X and Y cross is the same thing as the likelihood of both events occurring. As a result, the intersection of two or more occurrences is also known as the joint probability. Probability is a branch of statistics concerned with the chance of a certain event or phenomenon occurring. It is expressed as a number between 0 and 1, with 0 denoting an impossibility of occurrence and 1 denoting the certainty of an event’s outcome.
One is that occurrences X and Y must occur simultaneously. A good illustration would be throwing two dice. The other requirement is that occurrences X and Y be independent of one another. That is, the result of event X has no bearing on the outcome of event Y. Joint probability is a measure of two occurrences occurring at the same time, and it can only be used in circumstances when more than one observation is possible.
The occurrences must be independent in order for joint probability estimates to function. In other words, the occurrences must be independent of one another. To evaluate if two occurrences are independent or dependent, consider whether the outcome of one event would have an influence on the other’s outcome. The occurrences are independent if the outcome of one event has no bearing on the outcome of the other.
A probability distribution for two (or more) random variables is shown as a joint probability distribution. The standard is to utilize X and Y instead of A and B for events. Let A, B, and so on be random variables specified on a probability space. The joint probability distribution for A, B,….. is defined as the probability distribution that each of A, B,….. falls inside any specific range or discrete set of values supplied for that variable.
This is referred to as a bivariate distribution when just two random variables are present; otherwise, it is referred to as a multivariate distribution. The point where X and Y cross is the same thing as the likelihood of both events occurring. As a result, the intersection of two or more occurrences is also known as joint probability. The likelihood of clouds in the sky and the chance of rain on that day are two examples of dependent occurrences. The likelihood of rain on a given day is influenced by the presence of clouds in the sky. As a result, they are dependent events.
Joint probability is not to be confused with conditional probability, which is the likelihood of one occurrence occurring if another action or event occurs. Depending on the nature of the variable, the joint probability distribution can be represented in a variety of ways. A joint probability mass function can be represented in the case of discrete variables. It can be expressed in terms of a joint cumulative distribution function or a joint probability density function for continuous variables.
When there is a precondition that the event already exists or the event previously supplied has to be true, conditional probability occurs. It’s also possible to say that one event is contingent on the occurrence or presence of another. A probability distribution for two or more random variables is called a joint probability distribution. Both conditional and joint probability deal with two occurrences, but the order in which they occur distinguishes them.
It has an underlying condition in conditional, but it merely happens at the same moment in joint. The likelihood of A and B happening is equal to the probability of X happening given that Y happens multiplied by the probability of Y happening. Both occurrences must be independent of one another in order to calculate joint probability. The likelihood of obtaining “tails” or “heads” on a coin flip, for example, are separate occurrences. The chance of obtaining heads on two coin flips is an example of independent occurrences. The probability of getting a head on the first coin toss does not have an impact on the probability of getting heads on the second coin toss.
When two or more observable events can occur at the same time, statisticians and analysts utilize joint probability as a tool. For example, joint probability can be used to predict the possibility of a decrease in the Dow Jones Industrial Average (DJIA) followed by a dip in Microsoft’s stock price, or the likelihood of oil prices rising at the same time that the US currency falls.
Information Sources: