The Hoover index, also known as the Robin Hood index or the Schutz index, is one of the most basic inequality measures for determining departure from the ideal equal distribution. It’s the proportion of total community income that would have to be reallocated (taken from the wealthier half and given to the poorer half) in order to achieve income equality. The index is the proportion of communal revenue that would be taken from the wealthier half of the population and given to the poorer half in order for a society to be fully equal.
In a totally equivalent society, there would be no compelling reason to reallocate pay to accomplish an equivalent abundance dispersion. The Hoover index can be graphically addressed as the longest upward distance between the Lorenz bend, or the total part of the absolute pay held under a specific pay percentile, and the 45-degree line addressing wonderful fairness. It’s most commonly utilized in applications involving socioeconomic class (SES) and health. It is one of the most fundamental inequality indexes in econometrics.
The Gini coefficient, which is likewise based on the Lorenz curve, is a more well-known measure of inequality. In an economy where most of the abundance is amassed in the possession of a couple of people, most of that pay would require being rearranged (taken from the more extravagant) given to most of the populace that is poor to accomplish pay uniformity. The Hoover Index ranges from 0 to 1 (or 0% to 100%), with 0 being a completely equal society and 100 representing the most unequal society.
Income inequality measures are used by sociologists to evaluate income disparities among participants in a national or global economy. The distribution of factor income, which is the distribution of the primary elements of production such as land, capital, and labor, was a concern for classical economists such as David Ricardo and Adam Smith.
Modern economists have studied income redistribution throughout the economy in the same way that classical economists did, but with an emphasis on people and family units. The characteristics of an income inequality metric should be as follows:
- Population independence: The premise that the economy has a big or small population should not be used to calculate income disparity. It follows that the population size should not be used as a measure for measuring inequality. As a result, an economy with a small population should not be regarded as being more equal than one with a huge population.
- Transfer principle: This concept, also known as Pigou-Dalton, states that if income is moved from the affluent to the poor, the measured degree of inequality should not rise. Instead, since there has been activity to eliminate inequality and strive toward a completely equal society, inequality should decline.
- Anonymity/Symmetry: This assumption indicates that the measure should be based on the distribution of income rather than specific persons in the economy. For example, if two persons, Person A and B, own 70% and 30% of the wealth in an economy, the inequality statistic should be the same whether Person A or B owns 30%. As a result, the measure should be based on how money is divided rather than who the individuals in the economy are.
On a graph, the Hoover Index equals the largest vertical distance between the Lorenz Curve and the perfect equality line, which is a 45-degree line. The Hoover index value represents an estimate of the share of total community income that must be moved from families that are above the mean to households that are below the mean in order to achieve income distribution equality. On a graph, the relationship may be expressed as follows:
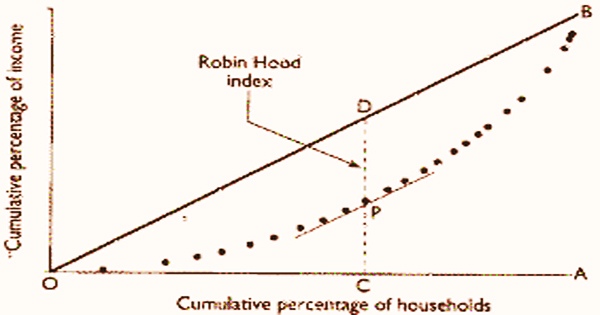
When the Hoover Index is applied to real-world allocation procedures, it does not imply that they take place in a perfectly planned economy. Rather, the index measures the gap between the existing system’s resource distribution to poorer participants and the eventual process of resource distribution to attain perfect income equality.
Information Sources: