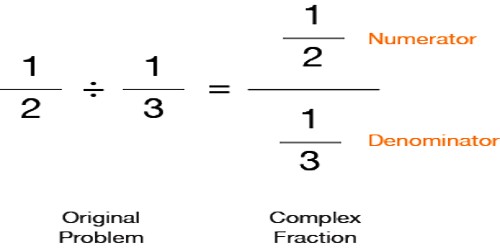
Dividing Fractions by Fractions
Dividing a fraction by a fraction might seem confusing at first, but it is really very simple.
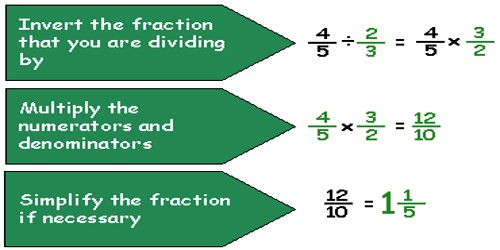
To Divide Fractions:
- Invert (i.e. turn over) the denominator fraction and multiply the fractions
- Multiply the numerators of the fractions
- Multiply the denominators of the fractions
- Place the product of the numerators over the product of the denominators
- Simplify the Fraction
This is the quickest technique for dividing fractions. The top and bottom are being multiplied by the same number and, since that number is the reciprocal of the bottom part, the bottom becomes one. Dividing anything by one leaves the value “anything” the same.
Example: Divide 2/9 and 3/12
- Invert the denominator fraction and multiply (2/9 ÷ 3/12 = 2/9 * 12/3)
- Multiply the numerators (2*12=24)
- Multiply the denominators (9*3=27)
- Place the product of the numerators over the product of the denominators (24/27)
- Simplify the Fraction (24/27 = 8/9)
The Easy Way. There is a lengthier way of dividing fractions and it could be said to be a “more correct” method. It involves the use of equivalent fractions to make the denominators of both fractions the same. This is the correct way since, strictly speaking you can’t divide apples by oranges in the same way as you can’t divide fifths by fourths. After inverting, it is often simplest to “cancel” before doing the multiplication. Canceling is dividing one factor of the numerator and one factor of the denominator by the same number.
For example: 2/9 ÷ 3/12 = 2/9*12/3 = (2*12)/(9*3) = (2*4)/(3*3) = 8/9
Information Source: