A researcher is publishing a new formula that helps find that equation quickly, based on the theory that for every action, even those that appear complex and random, there is a math problem that describes it. Yes, he is hastening science.
Consider a tall, stately grandfather clock, with its long pendulum swinging back and forth, keeping time. Scientists can describe the motion of the pendulum with an equation or a dynamical model, and while there appear to be hundreds of factors contributing to the sway, there is only one variable required to describe the motion of the pendulum and translate it into math: the swing angle. It is unknown how long it took scientists and mathematicians to discover this. It could have taken years to test each variable in the equation to determine the single important variable for sway.
A University of Houston researcher has now reported a method for describing these types of complex systems with the fewest number of variables possible, sometimes reducing the possibility of millions to a negligible number, and only one on rare occasions. It’s a breakthrough that, because of its efficiency and ability to understand and predict the behavior of natural systems, has the potential to accelerate a wide range of activities that rely on simulations, from weather forecasting to aircraft production.
Our method finds the very most compact description that is mathematically possible, and that’s what differentiates our method from others. Using ideas from machine learning and smooth manifold theory, the method makes simulations extremely fast and inexpensive.
Daniel Floryan
“In the example of the grandfather clock, I can take a video of the pendulum swinging back and forth and from that video, automatically discover what is the right variable. Accurate models of system dynamics enable deeper understanding of these systems, as well as the ability to predict their future behavior,” reports Daniel Floryan, Kalsi Assistant Professor of Mechanical Engineering, in the journal Nature Machine Intelligence.
To begin building the compact-yet-accurate models, one principle is fundamental: For every action, even those seemingly complex and random, there exists an underlying pattern that enables a compact representation of the system.
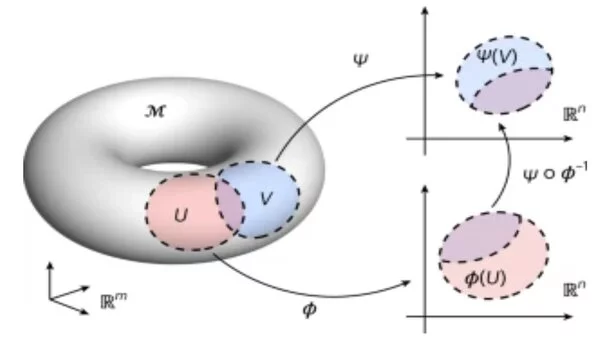
“Our method finds the very most compact description that is mathematically possible, and that’s what differentiates our method from others,” said Floryan.
Using ideas from machine learning and smooth manifold theory, the method makes simulations extremely fast and inexpensive.
Floryan simulated the reaction of two chemicals in one application. When the chemicals met, they displayed complex behavior: a repetitive rhythmic spiraling that required more than 20,000 variables to simulate. Floryan fed video of the reaction into his algorithm, which discovered that he only needed one variable to comprehend the action. The time it took the spiral to return to its starting point, like a second hand on a watch, was a necessary variable.
In the context of weather forecasting, numerical models are computer simulations of the atmosphere that employ complex physics and fluid dynamics equations.
“For weather prediction and climate modeling, if you have something that is much faster you can better model the earth’s climate and better predict what’s going to happen,” said Floryan.