A discrete distribution is a distribution of data with discrete values in statistics. In the case where the value range is countably infinite, these values must decrease to zero quickly enough for the probabilities to add up to 1. It is a statistical distribution showing the probability of discrete (countable) results, such as 1, 2, 3… There can be either discrete or continuous statistical distributions. Discrete values, such as 1, 10, 15, etc., are countable, finite, non-negative integers. Notable discrete probability distributions utilized in measurable demonstrating incorporate the Poisson dissemination, the Bernoulli appropriation, the binomial circulation, the mathematical dispersion, and the negative binomial dispersion.
A continuous distribution is constructed from results that fall within a continuum, such as all figures greater than 0 (which includes numbers whose decimals continue indefinitely, such as 3.14159265…). In addition, in computer programs that allow equal-probability random selections between a number of options, the discrete uniform distribution is widely used. At the point when an example (a bunch of perceptions) is drawn from a bigger populace, the example focuses have an exact circulation that is discrete, and which gives data about the populace dispersion. Overall, the underpinnings of probability theory and statistical analysis are the principles of discrete and continuous probability distributions and the random variables they represent.
Therefore, a discrete probability distribution is frequently addressed as a summed up likelihood thickness work including Dirac delta capacities, which considerably binds together the treatment of nonstop and discrete circulations. This is particularly useful when dealing with distributions of probability involving both a continuous component and a discrete part. In data analysis, distribution is a statistical term used. Statisticians trying to classify a specific study’s findings and probabilities can map observable data points from a data set, resulting in a diagram of the probability distribution. There are several forms of diagram shapes of a probability distribution that can arise from a distribution sample.
The two types of distributions are:
Discrete distributions: A discrete distribution, as referenced prior, is an appropriation of qualities that are countable entire numbers. Then again, a consistent circulation incorporates values with boundless decimal spots. Both distributions refer to distributions of probability, which are the basis of the theory of statistical analysis and probability.

Discrete Distribution Example
A probability distribution is a measurable capacity that is utilized to show all the potential qualities and probabilities of an arbitrary variable in a particular reach. The reach would be limited by most extreme and least qualities, yet the real worth would rely upon various variables. To illustrate where the expected value can end up, there are descriptive statistics used. The above probability distribution provides a visual representation of the probability that at any given hour a certain number of people will walk into the shop.
Continuous distributions: The development of either a discrete or continuous distribution can be defined by statisticians by the design of the effects to be calculated. A continuous distribution is a distribution of probabilities whose support, such as an interval in the real line, is an uncountable set. They are exceptionally portrayed by a cumulative distribution function that can be utilized to compute the likelihood for every subset of the help. There are numerous instances of continuous probability distributions: ordinary, uniform, chi-squared, and others. The probability density function (PDF) is the probability of a continuous random variable taking a given value by inferencing the region below the PDF from the sampled information and calculating it. While the absolute probability of a random variable taking a particular value is 0 (since infinite potential values exist), the probability of a random variable is inferred from the PDF in two separate samples.
It is regularly important to sum up the above definition for more self-assertive subsets of the genuine line. In these unique situations, a persistent likelihood conveyance is characterized as likelihood dissemination with a cumulative distribution function that is totally constant. Equivalently, with respect to the Lebesgue measure, it is a probability distribution on the real numbers that is totally continuous. It is possible to describe such distributions by their functions of probability density.
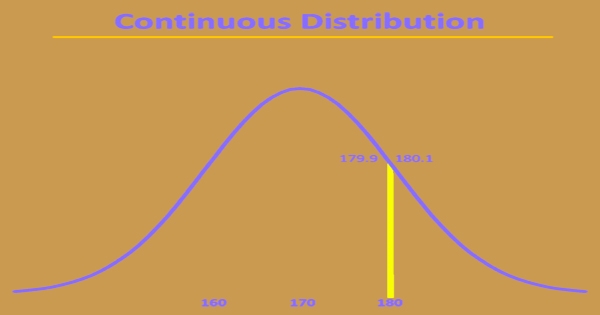
Continuous Distribution Example
Noticing the continuous distribution, unmistakably the mean is 170cm; nonetheless, the scope of qualities that can be taken is boundless. Subsequently, estimating the likelihood of some random irregular variable would require taking the derivation between two territories, as demonstrated previously. Binomial, Poisson, Bernoulli, and multi-nomial are the most common discrete probability distributions. One example where discrete distribution can be valuable for businesses is in inventory management. Studying the frequency of inventory sold in combination with a limited amount of available inventory will provide an organization with a distribution of probability that leads to guidance on the appropriate allocation of inventory to make the best use of square footage.
Discrete distributions additionally emerge in Monte Carlo simulations. A Monte Carlo simulation is a measurable displaying strategy that distinguishes the probabilities of various results by running a lot of reenactments. It is fundamentally used to help figure situations and recognize hazards. Outcomes with discrete values can generate discrete distributions for analysis in the Monte Carlo simulation. These distributions are used to assess risk and trade-offs between various things under consideration.
Information Sources: