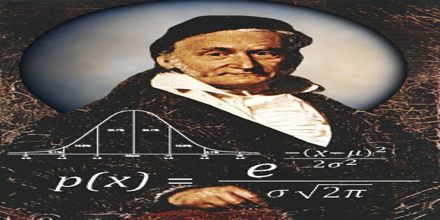Gauss’s personal life was overshadowed by the early death of his first wife, Johanna Osthoff, in 1809, soon followed by the death of one child, Louis. In primary school his teacher tried to occupy pupils by making them add a list of integers. The young Gauss reputedly produced the correct answer within seconds, to the astonishment of his teacher. Gauss’ presumed method, which supposes the list of numbers was from 1 to 100, was to realize that pairwise addition of terms from opposite ends of the list yielded identical intermediate sums: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101, and so on, for a total sum of 50 × 101 = 5050.
Carl Friedrich Gauss