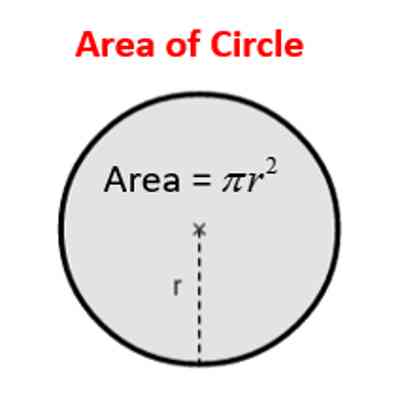
Area of a Circle
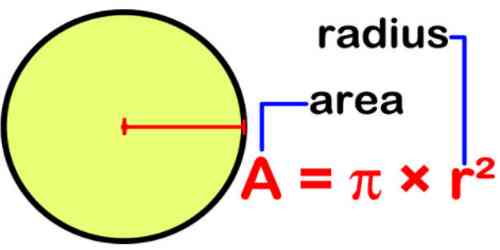
In geometry, the area enclosed by a circle of radius r is π r2. Here the Greek letter π represents a constant, approximately equal to 3.14159, which is equal to the ratio of the circumference of any circle to its diameter.
How to find the area of a circle
- The area of a circle can be found by multiplying pi ( π = 3.14) by the square of the radius
- If a circle has a radius of 4, its area is 3.14*4*4=50.24
- If you know the diameter, the radius is 1/2 as large.
The distance around a circle is called its circumference. The distance across a circle through its center is called its diameter. We use the Greek letter ‘π’ (pronounced Pi) to represent the ratio of the circumference of a circle to the diameter. In the last lesson, we learned that the formula for circumference of a circle is; C = πxd. For simplicity, we use ‘π’ = 3.14. We know from the last lesson that the diameter of a circle is twice as long as the radius. This relationship is expressed in the following formula; d = 2 x r.
The area of a circle is the number of square units inside that circle. If each square in the circle to the left has an area of 1 cm2, you could count the total number of squares to get the area of this circle. Thus, if there were a total of 28.26 squares, the area of this circle would be 28.26 cm2 However, it is easier to use one of the following formulas-
A = π.r2
where A is the area, and r is the radius.
Information Source: