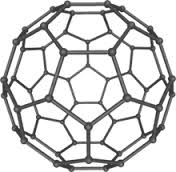
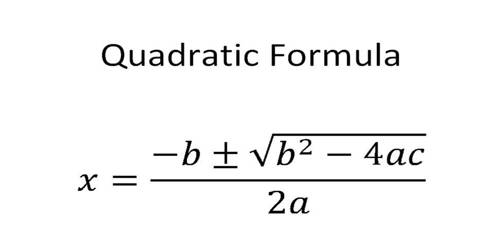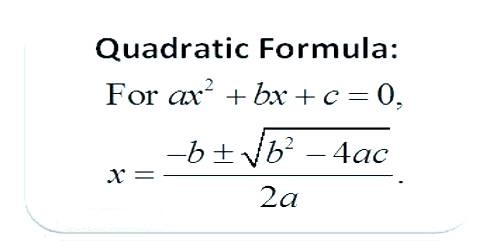The algebraic connectivity of a graph G is the second-smallest eigenvalue from the Laplacian matrix connected with G. This eigenvalue is in excess of 0 if and only if G is a connected graph. This is the corollary to the truth that the number of times 0 appears being an eigenvalue in the Laplacian is how many connected components inside the graph.
Algebraic Connectivity