Adding Fractions with Different Denominators
A very difficult area for many people is fractions, especially when you begin adding. This can become even more complex when the fractions have different denominators, or bottom numbers. Many people have difficulty adding fractions with unlike denominators. There’s no doubt that fractions are difficult to deal with especially when you have to find the least common denominator. In this article briefly describe how to Add Fractions with different denominators:
- Find the Least Common Denominator (LCD) of the fractions
- Rename the fractions to have the LCD
- Add the numerators of the fractions
- Simplify the Fraction
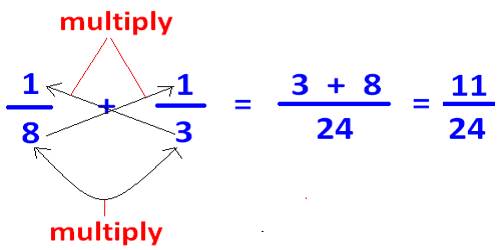
If the denominators are not the same, then you have to use equivalent fractions which do have a common denominator. To do this, you need to find the least common multiple (LCM) of the two denominators.
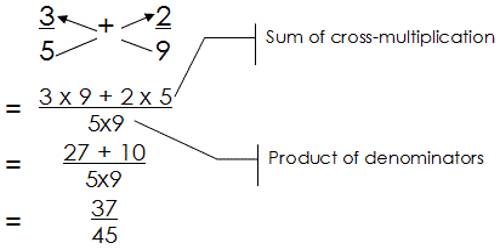
Steps for Adding Fractions with Unlike Denominators
- Identify the least common denominator by finding the least common multiple for the denominators.
- Write equivalent fractions (making sure that each equivalent fraction contains the least common denominator (LCM))
- Add the equivalent fractions that you wrote in step 2. (The denominators should now be the same.)
- Simplify if necessary.
Example: Find the Sum of 2/9 and 3/12
- Determine the Greatest Common Factor of 9 and 12 which is 3
- Either multiply the denominators and divide by the GCF (9*12=108, 108/3=36)
- OR – Divide one of the denominators by the GCF and multiply the answer by the other denominator (9/3=3, 3*12=36)
- Rename the fractions to use the Least Common Denominator(2/9=8/36, 3/12=9/36)
- The result is 8/36 + 9/36
- Add the numerators and put the sum over the LCD = 17/36
- Simplify the fraction if possible. In this case it is not possible
Information Source: