Volume of a Triangular Prism
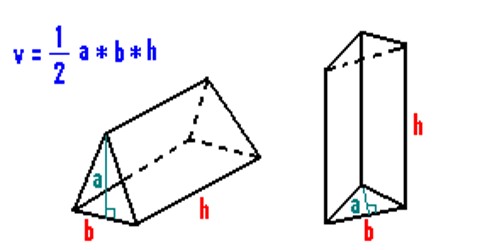
A triangular prism is a three-sided polyhedron with two parallel triangular bases and three rectangular faces. It should not be confused with a pyramid. If you want to calculate the volume of a triangular prism, all you have to do is find the area of one of the triangular bases and multiply it by the height of the shape.
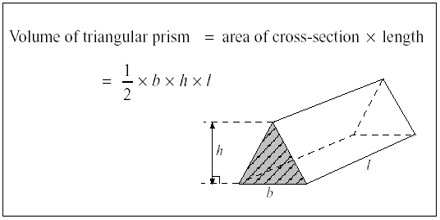
The volume of a triangular prism can be found by the formula:
Volume = [½ x length x width x height]
A triangular prism whose length is ‘l’ units, and whose triangular cross-section has base ‘b’ units and height ‘h’ units, has a volume of V cubic units given by;
V = ½ lbh
Example: Calculate the volume of a tent in the shape of a triangular prism having a length of 10 feet, the width of 8 feet and a height of 7 feet.
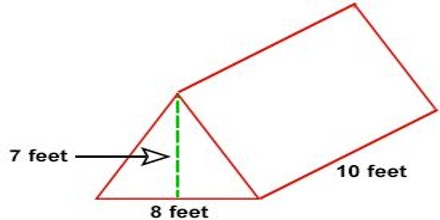
Solution: We obtain the following diagram –
Height of the prism = length of the tent
i.e. L = 10 feet
Length of base of triangle = width of tent
i.e. b = 8 feet
Height of the triangle = height of the tent
i.e. h = 7 feet
Formula for volume
V = ½ lbh
= ½ x 8 x 7 x 10
= 280 cubic feet.
Rules
The following rules should be kept in mind while calculating the volume of a triangular prism.
1) All the given values are to be denoted by the appropriate symbols with their units.
2) Determining the type of base triangle is useful.
3) The appropriate formula for finding the area of a triangle must be applied on the basis of a type of the triangle and the information given in the question.
4) Make sure that all the lengths must be represented by the same unit. In case they are not, use conversions to make them equal.
5) Writing unit of volume (unit3 or cubic unit) along with the answer is a must.
Information Source: Tutorvista