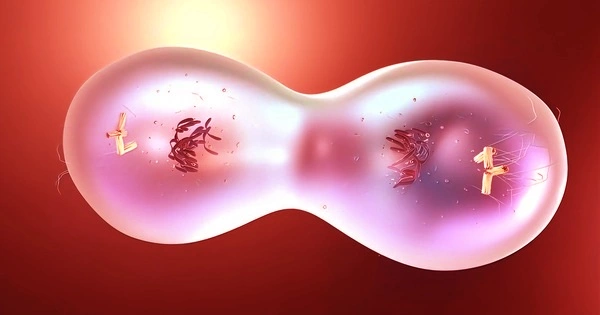
When dividing, how does a cell balance risk and speed? Scientists created and tested the first mathematical theory describing the cell’s best strategy for dividing safely and efficiently. Cells go through a life cycle in which they grow to the appropriate size, become equipped to perform their functions, and then divide into two new cells. The cell cycle is important because it ensures the survival of the cell population and, by extension, the larger structure of which it is a part, such as a tissue in the body.
Checkpoints tightly regulate the cell cycle, preventing errors such as mutations or DNA damage from being passed on to the next generation of cells. Each checkpoint serves as a quality-control monitor (a biological “checklist”), ensuring the cell cycle’s order, integrity, and fidelity. However, checkpoints frequently fail or are overridden after a prolonged halt in the cell cycle. If this occurs in the human body, it could lead to uncontrolled cell growth and division, as seen in cancer.
“When checkpoints detect problems, they can stop either the cell cycle or the organism’s development,” says Sahand Jamal Rahi of EPFL’s School of Basic Sciences. “However, if cells or organisms are stuck with an error for an extended period of time, they often continue dividing or growing; they do not stop forever. If checkpoints do not stop at all, there is a real risk of dying, but waiting forever is effectively equivalent to dying.”
When checkpoints detect problems, they can stop either the cell cycle or the organism’s development. However, if cells or organisms are stuck with an error for an extended period of time, they often continue dividing or growing; they do not stop forever.
Sahand Jamal Rahi
The math of checkpoint override
The question then is how the cell balances risk and speed when dividing. Despite its importance, checkpoint override is not well understood, neither theoretically nor experimentally. However, Rahi and his colleagues present the first mathematical theory to describe the process of checkpoint override in a new paper. “Many organisms must predict what will happen,” he says. “You have a problem, and you must determine how serious it is because the consequences are unknown. You might make it through, or you might not. As a result, the cell places a wager in either case. And the odds of that bet are examined in this study.”
The budding yeast Saccharomyces cerevisiae, which has been used in winemaking, baking, and brewing for centuries, was chosen as a real-life model organism by the researchers. “There are systems that monitor organisms, and perhaps the best studied of these systems is the DNA damage checkpoint in yeast,” Rahi says. “So we decided to take a look at it and see if we could make sense of checkpoint overrides. We began with a mathematical analysis that was based on a very simple question: what if these organisms are balancing risk and speed because they must predict the future?”
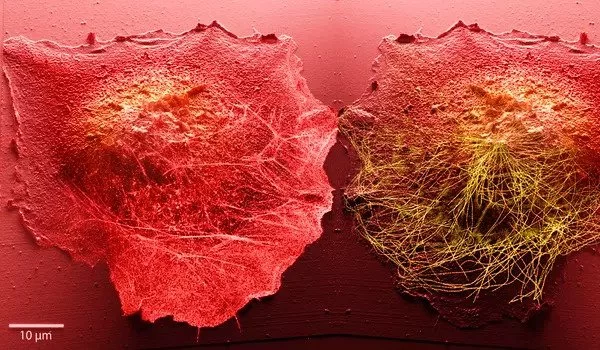
The risk-speed tradeoff
This tradeoff between risk and speed is analogous to the quality control system of a factory assembly line: how quickly can you produce things before the quality suffers? How do you strike the right balance between quality and efficiency? “People have previously considered this risk-speed tradeoff for checkpoints, but only qualitatively,” Rahi says. “It has not been studied or taken seriously. So I guess we can claim ownership of the concept!”
The scientists looked into the relationship between risk and speed. “The theory is basically balancing different probabilities, so we’re computing the change in fitness if you wait versus if you continue with self-replication,” says Rahi. “The organism has to come up with a strategy that involves continuously making the decision to wait or go depending on the gravity of the organism’s situation at that time. Of course, waiting means that you will make fewer and fewer progeny. So the alternative is to take a risk, so the cell divides and there’s a probability that it survives, and there’s a probability that it dies.” The theory calculates when risk and speed balance one another, determining the optimal “time.” “The result turned out to be a very simple equation,” Rahi adds.
Despite being developed for yeast, the theory is applicable to cells in general because it only considers risk and speed, which are factors that affect all organisms. “There isn’t a one-to-one correspondence between what happens in yeast and what happens in mammalian cells because mammalian cells have other constraints than just maximizing their own growth,” Rahi explains.
The cancer dimension
“However, when cells develop cancer, they decouple their fitness from that of their host.” Then, according to Darwinian evolution, they should redesign their checkpoints to maximize growth. It’s something we’re curious about; one of our next steps will be to see if cells rewire their checkpoints in an optimal way when they become cancerous.”
Rahi does not believe that cancerous cells will completely lose their checkpoint systems. “They don’t get rid of their checkpoints because it exposes them to too much risk in each division,” he explains. “Having no checkpoints at all compared to when they were precancerous is also not optimal because they will die as soon as there is a problem. So, we’re interested to see whether they too aim for this state of optimal balance that our theory describes.”