A topological insulator is a material that is an insulator inside but conducts electricity on its surface or edges. The topology of the material’s electronic band structure is responsible for this one-of-a-kind property. These insulators are a type of insulator that is distinct from all other types of insulators. These materials differ from ordinary insulators in that they have an inverted bulk gap for electronic excitations caused by strong spin-orbit coupling, ensuring the presence of gapless metallic boundary states similar to chiral edge modes in quantum Hall systems, but with helical spin textures.
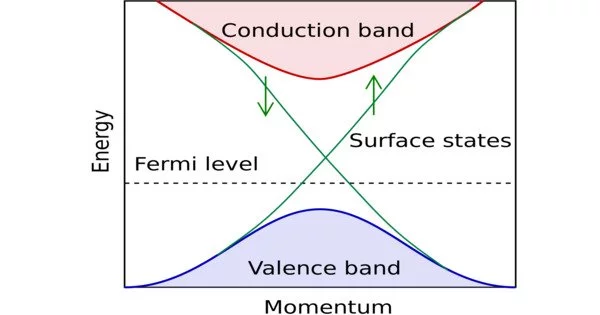
A topological insulator is a material with an electrical insulator interior and an electrical conductor surface, which means that electrons can only move along the material’s surface. It is an insulator for the same reason that a “trivial” (ordinary) insulator is: an energy gap exists between the material’s valence and conduction bands. However, in a topological insulator, these bands are “twisted” in comparison to a trivial insulator.
Without untwisting the bands, which closes the band gap and creates a conducting state, the topological insulator cannot be continuously transformed into a trivial one. Thus, due to the continuity of the underlying field, the border of a topological insulator with a trivial insulator (including vacuum, which is topologically trivial) is forced to support a conducting state.
The bulk of a topological insulator has an energy gap that prevents electron flow, whereas the surface or edge states have a band structure that allows electron flow. These topologically protected surface or edge states are resistant to defects and impurities that would normally scatter electrons in a conventional material.
Topological insulators have potential applications in a variety of fields, including electronics, spintronics, and quantum computing. They may also have applications in energy harvesting and storage, as well as in creating new types of sensors and detectors.
The topologically protected surface states of a topological insulator are of great interest because they have many unusual properties, such as a spin-momentum locking that makes them immune to backscattering, resulting in very high electron mobility. They can also have nontrivial topological properties, such as the presence of a Dirac cone, which is a linear dispersion relation between energy and momentum that is reminiscent of relativistic particles.
Overall, the discovery and study of topological insulators has opened up new avenues for research in condensed matter physics and has the potential to revolutionize various technological fields.