Theorem of Joint Variation
If x ∝ y when z is constant and x ∝ z when y is constant, then x ∝ yz when both y and z vary. If one variable varies as the product of other variables, it is called joint variation. The phrase “y varies jointly as x and z” is translated in two ways.
Proof
Since x ∝ y when z is constant Therefore x = ky where k = constant of variation and is independent to the changes of x and y.
Again, x ∝ z when y is constant.
or, ky ∝ z when y is constant (since, x = ky).
or, k ∝ z (y is constant).
or, k = mz where m is a constant which is independent to the changes of k and z.
Now, the value of k is independent to the changes of x and y. Hence, the value of m is independent to the changes of x, y and z.
Therefore x = ky = myz (since, k = mz)
where m is a constant whose value does not depend on x, y and z.
Therefore x ∝ yz when both y and z vary.
Note: (i) The above theorem can be extended for a longer number of variables. For example, if A ∝ B when C and D are constants, A ∝ C when B and D are constants and A ∝ D when B and C are constants, thee A ∝ BCD when B, C and D all vary.
(ii) If x ∝ y when z is constant and x ∝ 1/Z when y is constant, then x ∝ y when both y and z vary.
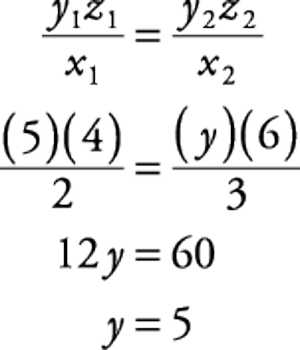
Some Useful Results
Theorem of Joint Variation
(i) If A ∝ B, then B ∝ A.
(ii) If A ∝ B and B∝ C, then A ∝ C.
(iii) If A ∝ B, then Aᵇ ∝ Bᵐ where m is a constant.
(iv) If A ∝ BC, then B ∝ A/C and C ∝ A/B.
(v) If A ∝ C and B ∝ C, then A + B ∝ C and AB ∝ C²
(vi) If A ∝ B and C ∝ D, then AC ∝ BD and A/C ∝ B/D
Now we are going to proof the useful results with step-by-step detailed explanation
Proof: (i) If A ∝ B, then B ∝ A.
Since, A ∝ B Therefore A = kB, where k = constant.
or, B = 1/K ∙ A Therefore B ∝ A. (since,1/K = constant)
Proof: (ii) If A ∝ B and B ∝ C, then A ∝ C.
Since, A ∝ B Therefore A = mB where, m = constant
Again, B ∝ C Therefore B = nC where n= constant.
Therefore A= mB = mnC = kC where k = mn = constant, as m and n are both Constants.
Therefore A ∝ C.
Proof: (iii) If A ∝ B, then Aᵇ ∝ Bᵐ where m is a constant.
Since A ∝ B Therefore A = kB where k= constant.
Aᵐ = KᵐBᵐ = n ∙ Bᵐ where n = kᵐ = constant, as k and m are both constants.
Therefore Aᵐ ∝ Bᵐ.
Results (iv), (v) and (vi) can be deduced by similar procedure.
Summarization:
(i) If A varies directly as B, then A ∝ B or, A = kB where k is the constant of variation. Conversely, if A = kB i.e., A/B = k where k is a constant, then A varies directly as B.
(ii) If A varies inversely as B, then A ∝ 1/B or, A= m ∙ 1/B or, AB= m where m = constant of variation. Conversely, if AB = k (a constant), then A varies inversely as B.
(iii) If A varies jointly as B and C, then A ∝ BC or A = kBC where k = constant of variation.
Information Source: