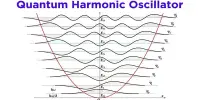
Statistical mechanics is the application of probability theory, which includes mathematical tools for dealing with large populations, to the field of mechanics, which is concerned with the motion of particles or objects when subjected to a force. It is a branch of physics that combines the principles and procedures of statistics with the laws of both classical and quantum mechanics. It also discusses the definition of certain equilibrium and time-dependent distribution functions of fundamental importance in the theory of liquids.
It was the first foundational physical theory in which probabilistic concepts and probabilistic explanation played a fundamental role. It provides a framework for relating the microscopic properties of individual atoms and molecules to the macroscopic or bulk properties of materials that can be observed in everyday life, therefore explaining thermodynamics as a natural result of statistics and mechanics (classical and quantum) at the microscopic level. It is a branch of statistical physics that deals with the description of physical phenomena in terms of the stochastic behavior of large numbers of components. It aims to predict and explain the measurable properties of macroscopic systems on the basis of the properties and behavior of the microscopic constituents of those systems. In particular, it can be used to calculate the thermodynamic properties of bulk materials from the spectroscopic data of individual molecules.
Statistical mechanics provides exact methods to connect thermodynamic quantities (such as pressure) to microscopic behavior. This ability to make macroscopic predictions based on microscopic properties is the main asset of statistical mechanics over thermodynamics. Both theories are governed by the second law of thermodynamics through the medium of entropy. However, entropy in thermodynamics can only be known empirically, whereas, in statistical mechanics, it is a function of the distribution of the system on its micro-states.