Slope of a Line
One of the most important properties of a straight line is in how it angles away from the horizontal. This concept is reflected in something called the “slope” of the line.
Concept of slope (or gradient):
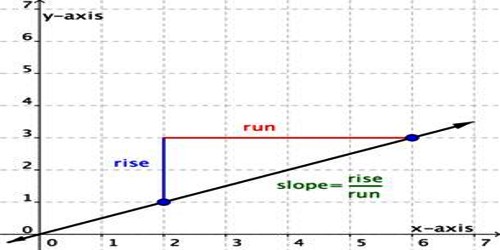
If θ (≠ 90°) is the inclination of a straight line, then tan θ is called its slope or gradient. The slope of any inclined plane is the ratio between the vertical rise of the plane and its horizontal distance.
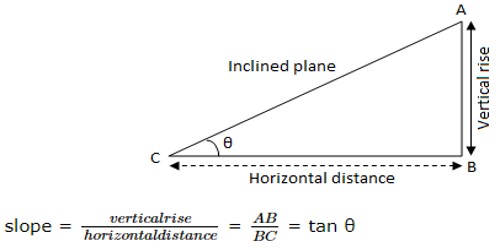
Where θ is the angle which the plane makes with the horizontal
Slope of a straight line:
The slope of a straight line is the tangent of its inclination and is denoted by letter ‘m’ i.e. if the inclination of a line is θ, its slope m = tan θ.
Remember:
Direction is important when it comes to determining slope. It’s important to pay attention to whether you are moving up, down, left, or right; that is, if you are moving in a positive or negative direction. If you go up to get to your second point, the rise is positive. If you go down to get to your second point, the rise is negative. If you go right to get to your second point, the run is positive. If you go left to get to your second point, the run is negative.
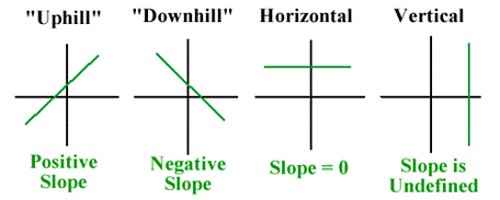
(i) The slope of a line is positive if it makes an acute angle in the anti-clockwise direction with x-axis
(ii) The slope of a line is negative, if it makes an obtuse angle in the anti-clockwise direction with the x-axis or an acute angle in the clockwise direction with the x-axis.
(iii) Since tan θ is not defined when θ = 90°, therefore, the slope of a vertical line is not defined. i.e., slope of y-axis is m = tan 90° = ∞ i.e., not defined.
(iv) Slope of x-axis is m = tan 0° = 0
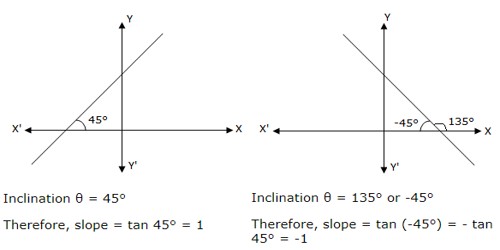
(v) Since the inclination of every line parallel to x-axis is 0°, so its slope (m) = tan 0° = 0. Therefore, the slope of every horizontal line is 0.
It does not matter which of the two “slope” formulas you use, nor does it matter which point you pick to be your “first” and which you pick to be your “second”. The only thing that matters is that you subtract your x-values in the same order as you had subtracted your y-values.
Information Source: