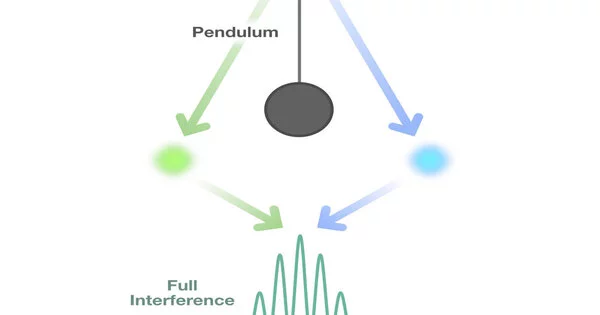
The quantum pendulum is critical to understanding hindered internal rotations in chemistry, quantum features of scattering atoms, and a variety of other quantum phenomena. It is a theoretical model that combines concepts from classical mechanics and quantum mechanics to describe the quantum-level behavior of a pendulum. A pendulum is described in classical mechanics by its position and momentum, and its motion is governed by Newton’s laws of motion. Despite the fact that a pendulum not subject to the small-angle approximation has inherent nonlinearity, the Schrödinger equation for the quantized system is relatively simple to solve. Particles, on the other hand, are described by wave functions in quantum mechanics and exhibit wave-particle duality.
A wave function, which represents the probability distribution of finding the pendulum at different positions, describes the motion of a quantum pendulum. The wave function changes with time according to the Schrödinger equation, which determines how the wave function of a pendulum changes with time.
The concept of superposition is one of the key differences between a classical pendulum and a quantum pendulum. A particle in quantum mechanics can exist in a superposition of multiple states at the same time. This means that a quantum pendulum can be in a superposition of different positions, oscillating between different points in space.
The wave function collapses when the quantum pendulum is observed or measured, and the pendulum is found in a specific position with a certain probability. The act of measuring disturbs the state of the pendulum, and subsequent measurements may yield different results.
Quantum pendulums are primarily theoretical models used to study the behavior of quantum systems and to comprehend quantum mechanics principles. They illuminate the wave-like nature of particles as well as the probabilistic nature of quantum measurements. It is important to note, however, that building a physical system that exhibits all of the characteristics of a quantum pendulum can be difficult because it requires precise control over quantum systems and their interactions.
Making measurements on a quantum pendulum’s properties, such as its position or momentum, would be required to observe it. However, due to the uncertainty principle in quantum mechanics, it is impossible to know the exact position and momentum of a quantum system at the same time. Measuring a quantum pendulum would thus produce probabilistic results, with the probability distribution determined by the wavefunction.