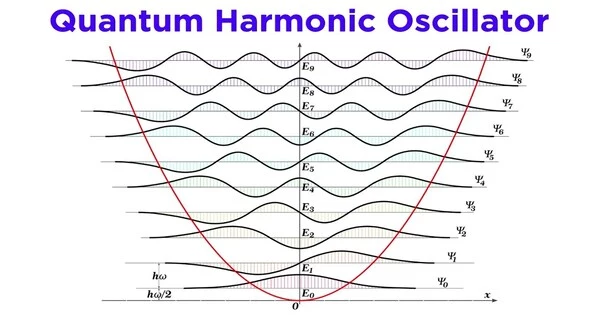
A fundamental model in quantum mechanics that describes the behavior of a particle in a harmonic potential well is the quantum harmonic oscillator. It is the classical harmonic oscillator’s quantum-mechanical counterpart. One of the most important model systems in quantum mechanics is an arbitrary smooth potential, which can usually be approximated as a harmonic potential near a stable equilibrium point. It represents various physical systems, such as molecular vibrations, atomic force fields, and quantum field theory, in a simplified manner. It is also one of the few quantum-mechanical systems for which an exact, analytical solution exists.
A harmonic oscillator is a mass attached to a spring that oscillates back and forth due to the force exerted by the spring. The mass’s displacement from its equilibrium position follows a sinusoidal pattern. However, due to the wave-particle duality of quantum particles, the behavior of the harmonic oscillator differs in quantum mechanics. In contrast to the continuous energy spectrum of a classical oscillator, the quantum harmonic oscillator has discrete energy levels.
The Hamiltonian operator for the quantum harmonic oscillator is given by:
H = (ħω/2)(a†a + aa†)
where ħ is the reduced Planck’s constant, ω is the angular frequency of the oscillator, and a and a† are the annihilation and creation operators, respectively. These operators are associated with the ladder operators that raise and lower the energy levels of the system.
The energy eigenstates of the quantum harmonic oscillator are described by the Hermite polynomials, and the energy spectrum is given by E_n = (n + 1/2)ħω, where n is a non-negative integer representing the quantum number. The ground state, corresponding to n = 0, has the lowest energy.
The position and momentum operators for the quantum harmonic oscillator can be expressed in terms of the annihilation and creation operators. The position operator is given by:
x = (ħ/2mω)^0.5(a + a†)
and the momentum operator is:
p = i(ħmω/2)^0.5(a – a†)
where m is the mass of the particle.
The quantum harmonic oscillator is characterized by the following key features:
- Energy Levels: The energy levels of the quantum harmonic oscillator are discrete and quantized. The lowest energy level, called the ground state, has a non-zero energy, unlike in classical physics.
- Wave Functions: The wave functions of the quantum harmonic oscillator are described by Hermite polynomials. These wave functions represent the probability distribution of finding the particle at a particular position.
- Zero-Point Energy: The quantum harmonic oscillator’s ground state has a minimum energy known as zero-point energy. It is caused by the Heisenberg uncertainty principle, which states that a particle’s position and momentum cannot be known with perfect precision at the same time.
- Equidistant Energy Spacing: The quantum harmonic oscillator’s energy levels are equally spaced. The energy difference between successive levels is constant and is determined by the oscillator’s fundamental parameters, such as mass and force constant.
The quantum harmonic oscillator is an important model because it has analytical solutions that allow for detailed calculations and theoretical analysis. It serves as a foundation for understanding more complex quantum systems and is widely used in physics and chemistry.