QHE: Quantum Hall Effect
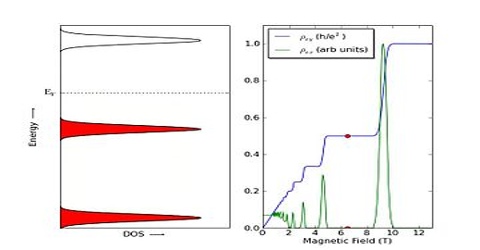
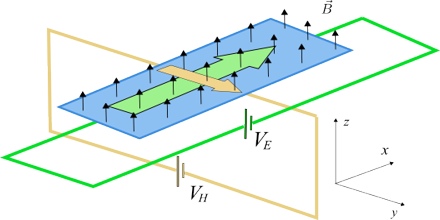
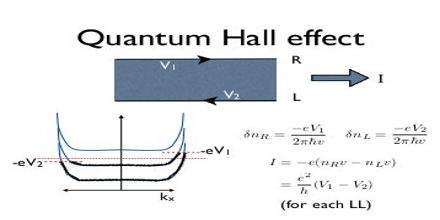
Quantum Hall Effect is a quantum-mechanical version of the Hall Effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductance σ undergoes quantum Hall transitions to take on the quantized values.
The discovery of the Quantum Hall Effect (QHE) was the result of systematic measurements on silicon field effect transistors-the most important device in microelectronics. Such devices are not only important for applications but also for basic research. The pioneering work by Fowler, Fang, Howard and Stiles has shown that new quantum phenomena become visible if the electrons of a conductor are confined within a typical length of 10 nm. Their discoveries opened the field of two-dimensional electron systems which since 1975 is the subject of a conference series.
In addition to the quantum phenomena connected with the confinement of electrons within a two-dimensional layer, another quantization – the Landau quantization of the electron motion in a strong magnetic field – is essential for the interpretation of the Quantum Hall Effect.
Applications of Quantum Hall Effect
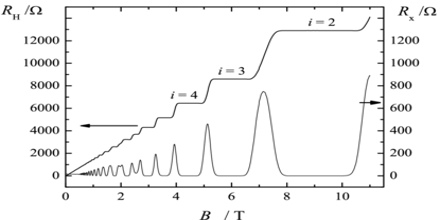
The quantization of the Hall conductance has the important property of being exceedingly precise. Actual measurements of the Hall conductance have been found to be integer or fractional multiples of e2/h to nearly one part in a billion. This phenomenon, referred to as “exact quantization”, has been shown to be a subtle manifestation of the principle of gauge invariance. It has allowed for the definition of a new practical standard for electrical resistance, based on the resistance quantum given by the von Klitzing constant RK = h/e2 = 25812.807557(18) Ω. This is named after Klaus von Klitzing, the discoverer of exact quantization. Since 1990, a fixed conventional value RK-90 is used in resistance calibrations worldwide. The Quantum Hall Effect also provides an extremely precise independent determination of the fine structure constant, a quantity of fundamental importance in quantum electrodynamics.
It’s useful to distinguish between two different Quantum Hall Effects which are associated to two related phenomena. These are called the integer and fractional quantum hall effects. Both were first discovered experimentally and only subsequently understood theoretically.
Materials of Quantum Hall Effect
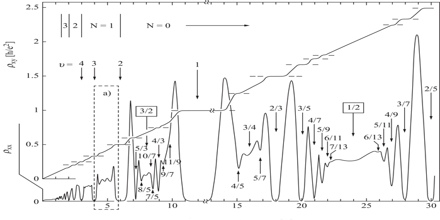
The integer Quantum Hall Effect was originally discovered in a Si MOSFET (this stands for “metal-oxide-semiconductor field-effect transistor”). This is a metal-insulator-semiconductor sandwich, with electrons trapped in the “inversion band” of width ∼ 30˚A between the insulator and semi-conductor. Meanwhile the fractional Quantum Hall Effect was discovered in a GaAs-GaAlAs heterostructure. A lot of the subsequent work was done on this system, and it usually goes by the name GaAs (Gallium Arsenide). In both these systems, the density of electrons is around n ∼ 1011 − 1012 cm−2.
Mathematics of Quantum Hall Effect
The integers that appear in the Hall Effect are examples of topological quantum numbers. They are known in mathematics as the first Chern numbers and are closely related to Berry’s phase. A striking model of much interest in this context is the Azbel-Harper-Hofstadter model whose quantum phase diagram is the Hofstadter butterfly shown in the figure. The vertical axis is the strength of the magnetic field and the horizontal axis is the chemical potential, which fixes the electron density. The colors represent the integer Hall conductances. Warm colors represent positive integers and cold colors negative integers. The phase diagram is fractal and has structure on all scales. In the figure there is an obvious self-similarity.
Concerning physical mechanisms, impurities and/or particular states are important for both the ‘integer’ and ‘fractional’ effects. In addition, Coulomb interaction is also essential in the fractional quantum Hall effect. The observed strong similarity between integer and fractional quantum Hall effects is explained by the tendency of electrons to form bound states with an even number of magnetic flux quanta, called composite fermions.
Nobel Prize of Quantum Hall Effect
The integer Quantum Hall Effect can be understood using free electrons. In contrast, to explain the fractional quantum Hall effect we need to take interactions between electrons into account. This makes the problem much harder and much richer. The basics of the theory were first laid down by Laughlin3 , but the subject has since expanded in a myriad of different directions. The 1998 Nobel Prize was awarded to Tsui, St¨ormer and Laughlin. Sections 3 onwards will be devoted to aspects of the fractional Quantum Hall Effect.