Negative convexity occurs when the yield curve of a bond is concave rather than convex; this is seen in mortgage-backed bonds and callable corporate bonds. Bond prices grow when interest rates decrease; conversely, a bond with negative convexity loses value as interest rates fall. The second derivative of a bond’s price with regard to its yield is used to calculate its convexity, which is the rate of change of its duration.
Convexity portrays how much a security’s span changes when financing costs change, implying that financial backers can gain so much not simply from the bearing of the yield bend however the breathtaking quality of the yield bend. To completely comprehend negative convexity, first get convexity, security costs, security yields, loan fees, and security terms. The convexity of a bond can be used to evaluate and manage a portfolio’s exposure to market risk. Bond prices and interest rates have a negative connection.
As a result, convexity aids investors in predicting what would happen to a bond’s price if market interest rates fluctuate. The length of a bond relates to how much the price of the bond is affected by interest rate changes. Convexity is the proportion of the arch in the connection between a security’s yield and its cost. It represents how, as loan costs change, the span of a bond varies.
When interest rates fall, the price of a bond usually rises. Bonds with negative convexity, on the other hand, see their prices decline when interest rates fall. Prepayment returns capital early, giving investors with the option of reinvesting at today’s reduced rates. There is a negative link or relationship between bond prices and interest rates:
- As interest rates grow or rise, bond prices decrease or fall.
- When interest rates decrease or fall, bond prices grow.
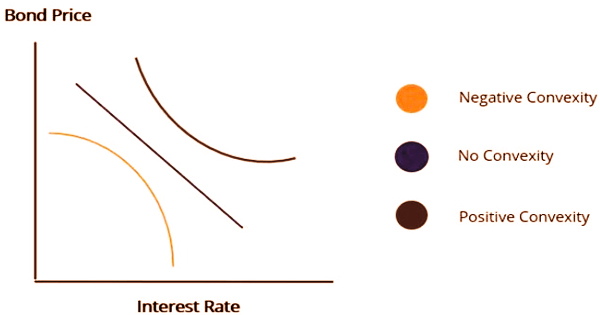
The negative link can be explained by the idea that when interest rates rise, the bond’s profits may fall behind. Investors, analysts, and traders assess a bond’s convexity since the duration is an imprecise price change estimate. Convexity is a valuable danger the executive’s instrument and is utilized to quantify and deal with a portfolio’s openness to advertising hazard. This assists with expanding the precision of value development expectations.
Bonds entering the market with greater yields will be issued at new, higher rates as interest rates climb. While the precise formula for convexity is fairly difficult, the following simple formula can be used to approximate convexity:
Convexity approximation = (P(+) + P(-) – 2 × P(0)) / (2 × P(0) × dy ^2)
Where:
P(+) = bond price when the interest rate is decreased
P(-) = bond price when the interest rate is increased
P(0) = bond price
dy = change in interest rate in decimal form
As rates increment, financial backers request a more noteworthy yield from the securities they buy. Subsequently, when financing costs rise, backers of such instruments ought to likewise raise their respects to stay serious. The majority of mortgage bonds are negatively convex, owing to the fact that they may be repaid. A bond’s price will fluctuate in the inverse direction of interest rate variations to a larger extent if the term is long.
At certain prices and yields, callable bonds can also display negative convexity. The reverse is also true: a shorter-term indicates less volatility in the bond price. An investor can use the following formula to predict a bond’s price for a given change in interest rates by combining duration and convexity:
Bond price change = duration × yield change + convexity adjustment
Convexity may be used to evaluate a bond’s risk level; the higher the convexity, the more sensitive the bond’s price is to interest rate changes. On the off chance that two securities are being dissected for venture purposes and they have practically identical yields and lengths, the security with the higher convexity is ideal in falling or stable loan fee conditions, as the adjustment of cost is bigger. Truth be told, the cost may really drop as it ends up being unmistakable that the bond will be called.
Information Sources: