Mathematics, histology, and genomes all agree that the most aggressive clear-cell renal cell carcinomas have low intratumor heterogeneity, meaning they have fewer different cell types. The study, led by UPV/EHU Ikerbasque Research Professor Annick Laruelle, supports the hypothesis that therapeutic strategies to maintain high levels of cellular heterogeneity within the tumor would be beneficial in slowing the evolution of the cancer and improving survival.
Mathematical techniques are gaining acceptance in modern oncology because they provide new insights into the evolution of cancer and new avenues for therapeutic advancement. As a result, data from mathematical studies support several of the histology and genetic findings.
For example, game theory can help us comprehend the “social” interactions that occur between cancer cells. This innovative viewpoint enables the scientific and clinical communities to comprehend the disease’s hidden events. In reality, viewing a tumor as a collection of individuals governed by previously determined ecological laws opens up new therapeutic avenues for patients.
It is a decision theory in which the outcome is dependent not only on one’s own decision, but also on the decision of the other actors. In the game, cells may act aggressively, like a hawk, or passively, like a dove, to acquire a resource.
Annick Laruelle
The hawk-dove game is a mathematical tool developed within the framework of game theory to analyze cooperation and rivalry in biology. When applied to cancer cell collectivities, it explains how tumor cells may behave when vying for an external resource. “It is a decision theory in which the outcome is dependent not only on one’s own decision but also on the decision of the other actors,” noted Annick Laruelle, an expert in game theory at the UPV/EHU’s Department of Economic Analysis. “In the game, cells may act aggressively, like a hawk, or passively, like a dove, to acquire a resource.”
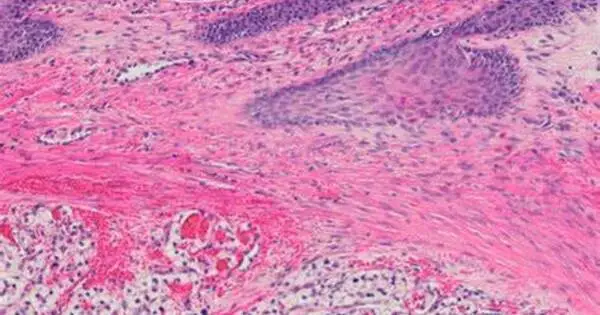
Professor Laruelle has used this game to analyze bilateral cell interactions in highly aggressive clear cell renal cell carcinoma in two different scenarios: one involving low tumour heterogeneity, when only two tumour cell types compete for a resource; and the other, high tumour heterogeneity, when such competition occurs between three tumour cell types. Clear cell renal cell carcinoma is so named because the tumour cells appear clear, like bubbles, under the microscope. This type of carcinoma has been taken as a representative case for the study, as it is a widely studied paradigm of intratumour heterogeneity (which refers to the coexistence of different subpopulations of cells within the same tumour).
Fresh theoretical approach for new therapeutic strategies
Laruelle has thus shown how some of the fundamentals of intratumour heterogeneity, corroborated from the standpoint of histopathology and genomics, are supported by mathematics using the hawk-dove game. The work, carried out in collaboration with researchers from Biocruces, the San Giovanni Bosco Hospital in Turin (Italy) and the Pontificia Universidade Catolica do Rio de Janeiro has been published in the journal Trends in Cancer by the Ikerbasque Research Professor.
According to the researchers, “this convergence of findings obtained from very different disciplines reinforces the key role of translational research in modern medicine and gives intratumour heterogeneity a key position in the approach to new therapeutic strategies” as well as suggesting that “intratumour heterogeneity behaves by following similar pathways in many other tumours.”
This could have serious ramifications for the clinical management of malignant tumors. In the age of precision oncology, the constant advent of novel compounds expands cancer treatment options. However, the researchers state that “discovering a new molecule is one thing; finding the best strategy for using it is quite another.” So far, the proposed method is predicated on giving the patient the highest acceptable dose.
This technique, however, encourages tumor cells to develop resistance as soon as possible, converting the original tumor into a neoplasm with limited intratumor heterogeneity composed of only resistant cells.” According to this theoretical approach, a therapy aimed primarily at preserving high intratumor heterogeneity may make sense, as it may limit cancer progression and hence contribute to prolonged survival. This viewpoint is currently gaining traction in oncology.