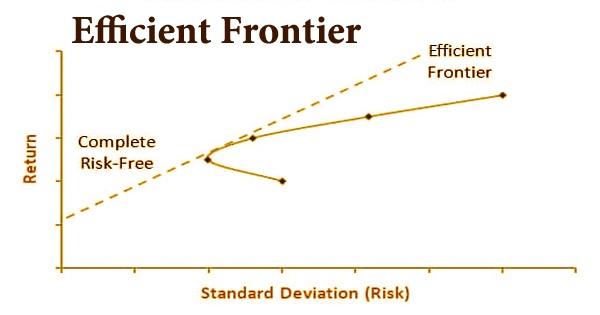
The efficient frontier, also known as the portfolio frontier in modern portfolio theory, is a collection of ideal or optimal portfolios that are supposed to give the highest return for the lowest risk. If there is no other portfolio that provides higher returns for a lower or equivalent amount of risk, it is said to be effective. Where portfolios are situated on the effective wilderness relies upon the financial backer’s level of hazard resistance. It is a speculation portfolio that possesses the “efficient” portions of the danger bring range back. Portfolios that cluster to the right of the efficient frontier have a higher level of risk for the given rate of return, making them sub-optimal.
The efficient frontier is a bended line. It is on the grounds that each expansion in hazard brings about a moderately more modest measure of profits. This frontier is shaped by plotting the normal profit from the y-axis and the standard deviation as a proportion of hazard on the x-axis. It demonstrates how a portfolio’s risk and return trade-off works. In other words, the marginal return to risk is decreasing, resulting in a curve. The effective frontier’s optimal portfolios have a higher degree of diversification than other portfolios.
In the Journal of Finance, Harry Markowitz published a systematic portfolio selection model in 1952. Over the next two decades, he continued to establish and publish research on the subject, eventually winning the Nobel Prize in Economics in 1990 for his work on the efficient frontier and other contributions to modern portfolio theory. The efficient frontier is addressed by plotting the normal returns of a portfolio and the standard deviation of profits. The y-axis is comprised of the normal returns of the portfolio. The x-axis is marked as the standard deviation of profits, which is a proportion of hazard.
Three critical considerations must be taken into account when constructing the frontier:
- Expected return,
- Variance/ Standard Deviation as a measure of the variability of returns also known as risk and
- The covariance of one asset’s return to that of another asset.
A portfolio of assets is said to be “efficient” if it has the best possible expected level of return for its level of risk (which is represented by the portfolio’s return standard deviation). Portfolios that optimize returns for the risk taken are represented graphically by the efficient frontier. Returns are subject to the speculation blends that make up the portfolio. In the event that a portfolio is plotted on the correct side of the graph, it demonstrates that there is a more elevated level of hazard for the given portfolio. On the off chance that it is plotted low on the chart, the portfolio offers low returns.
According to Markowitz, there is at least one portfolio that can be built from all available assets that has the estimated risk and return corresponding to that point on the productive frontier. The following is an example. Take note of how the efficient frontier helps investors understand how the projected returns of a portfolio differ depending on the amount of risk taken.
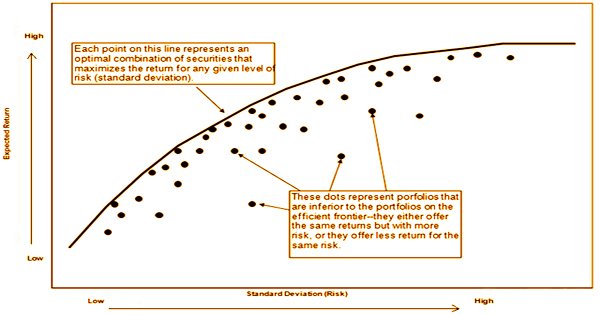
The efficient frontier is the establishment for the present-day portfolio hypothesis, which is the way financial backers mean to make a portfolio that amplifies expected returns dependent on a particular degree of hazard. Furthermore, Markowitz’s theory is predicated on many assumptions, including that investors are reasonable and want to avoid risk wherever possible; that there are insufficient investors to manipulate stock prices; and that investors have unrestricted access to borrowing and lending capital at the risk-free interest rate. Here, each conceivable mix of hazardous resources can be plotted in hazard expected return space, and the assortment of all such potential portfolios characterizes an area in this space. Without the chance to hold a danger free resource, this district is the chance set (the attainable set).
Markowitz’s hypothesis is based on the idea that investors would select portfolios that produce the highest possible returns with the least amount of risk, whether on intent or by accident. To put it another way, they look for portfolios that are on the productive frontier. It assists financial backers with understanding the likely dangers and returns in their portfolios and examine how they contrast with the ideal arrangement of portfolios that are viewed as productive. By knowing the level of risk associated with each portfolio, investors may adjust their investment strategies accordingly.
Truth, on the other hand, demonstrates that the market contains irrational and risk-seeking investors, large market players with the ability to manipulate market prices, and investors with restricted access to borrowing and lending capital. Investors are logical and have a thorough understanding of all market data. This presumption infers that every one of the financial backers are sufficiently careful to comprehend the stock developments, foresee returns, and contribute appropriately. That additionally implies that this model expects all financial backers to be in total agreement all things considered.
The “efficient frontier” is the positively sloped (upward-sloped) top boundary of this region, which is a portion of a hyperbola. When it comes to investing, one common belief is that a higher level of risk equals a higher potential return. Investors who take on a low level of risk, on the other hand, have a low potential return. It ought to be noticed that there is no single efficient frontier for everybody. Everyone is distinctive for each financial backer since it relies upon numerous components like the quantity of resources in the portfolio, the business of the resources, and the level of the financial backer’s danger resilience.
According to Markowitz’s theory, there is an ideal portfolio that can be constructed with a perfect risk-reward balance. When a risk-free asset is open, the opportunity set expands, and the productive frontier is a straight-line segment originating from the vertical axis at the value of the risk-free asset’s return and tangent to the risky-assets-only opportunity set. All financial backers have a shared objective, and that is to keep away from the danger since they are hazard opposed and boost the return quite far and practicable.
Securities with the highest potential returns or low-risk securities do not make up the best portfolio. Its aim is to strike a balance between securities with the highest potential returns and a reasonable level of risk, and securities with the lowest risk for a given level of potential return. There are very few financial backers who might influence the market cost. The choices of the financial backers are constantly founded on anticipated return and standard deviation as a proportion of hazard.
The efficient frontier is based on assumptions that may or may not be valid representations of real-world situations. It assumes, for example, that all investors are fair and avoid taking risks. It also assumes that stock price fluctuations are unaffected by the number of investors, and that all investors have fair access to risk-free borrowing. The hypothesis can be applied, or the frontier can be developed just when there is an idea of broadening included. For a situation where there is no broadening, it is certain that the hypothesis would fall flat. Such suppositions are not in every case valid, as certain investors may not settle on objective choices, and a few financial backers are high-daring people.
Securities on the left end of the productive frontier, on the other hand, would be ideal for risk-averse investors. Furthermore, it is a mistake to assume that investors have limitless borrowing and lending potential. It’s possible that the assumption that assets follow a typical distribution pattern isn’t always right. Actually, securities may need to encounter returns that are far away from the individual standard deviations, at times like three standard deviations from the mean. Not all financial backers acquire equivalent admittance to getting cash too. To summarize, the efficient frontier shows a collection of assets that provides the best potential return for a given level of risk. It is based on the past, and it changes every year; new data is available. After all, the statistics of the past do not have to repeat themselves in the future.
Information Sources: