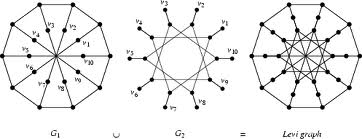
Primary objective of this lecture is to analysis Discrete Mathematics and its Applications based on Trees. A tree is often a connected undirected graph without any simple circuits. Brief hypothesis: An undirected graph is often a tree if and only if there is a unique simple way between any two associated with its vertices. Here briefly explain Internal Vertex and Binary Tree. Here also analysis on Ancestors: The ancestors of a non-root vertex are all the vertices in the path from root to this vertex and Descendants: The descendants of vertex v are all the vertices that have v as an ancestor. Finally discuss Traversal Algorithms with examples.
Discrete Mathematics and its Applications based on Trees