In mathematics, logarithms were developed for making complicated calculations simple. In mathematics, the logarithm is the inverse operation to exponentiation, just as division is the inverse of multiplication and vice versa. That means the logarithm of a number is the exponent to which another fixed number, the base, must be raised to produce that number.
For example, if a right circular cylinder has radius r = 0.375 meters and height h = 0.2321 meters, then its volume is given by: V = A = πr2h = 3.146 × (0.375)2 × 0.2321. Use of logarithm tables makes such calculations quite easy. However, even calculators have functions like multiplication; power etc. still, logarithmic and exponential equations and functions are very common in mathematics.
Antilogarithm is the number of which a given number is the logarithm.
If log M = x, then M is called the antilogarithm of x and is written as M = antilog x.
For example, if log 39.2 = 1.5933, then antilog 1.5933 = 39.2.
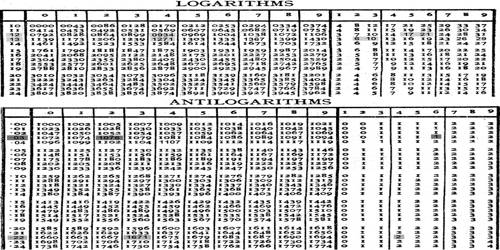
If the logarithmic value of a number is given then the number can be determined from the antilog-table. Antilog-table is similar to log-table; the only difference is in the extreme left-hand column which ranges from .00 to .99.
Example on antilogarithm:
- Find antilog 2.5463.
Solution:
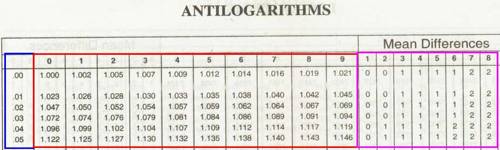
Clearly, we are to find the number whose logarithm is 2.5463. For this consider the mantissa .5463. Now find .54 in the extreme left-hand column of the antilog-table (see four-figure antilog-table) and then move horizontally to the right to the column headed by 6 of the top-most row and read the number 3516. Again we move along the same horizontal line further right to the column headed by 3 of mean difference and read the number 2 there. This 2 is now added to the previous number 3516 to give 3518. Since the characteristic is 2, there should be three digits in an integral part of the required number.
Therefore, antilog 2.5463 = 351.8.
- If log x = -2.0258, find x.
Solution:
In order to find the value of x using antilog-table, the decimal part (i.e., the mantissa) must be made positive. For this we proceed as follows:
log x = -2.0258 = – 3 + 3 – 2.0258
= – 3 + .9742 =3.9742
Therefore, x = antilog 3.9742.
Now, from antilog table, we get the number corresponding to the mantissa
.9742 as (9419 + 4) = 9423.
Again the characteristic in log x is (- 3).
Hence, there should be two zeroes between the decimal point and the first significant digit in the value of x.
Therefore, x = .009423.
Information Source: