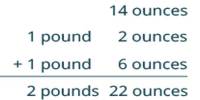
Additive Axiom

Additive Axiom: If a = b and c = d then a + c = b + d. If two quantities are equal and an equal amount is added to each, they are still equal.

The additive property of equality states that if the same amount is added to both sides of an equation, then the equality is still true. Let a, b, and c be real numbers, which consist of rational numbers (e.g., 0, -7, and 2/3) and irrational numbers (e.g., pi and the square root of 5). In symbols, we can say the following:

If a = b, then a + c = b + c.

Examples of the Additive Property of Equality

Let’s start with the following true equation:

5 = 5

Next, we will add 3 to each side of the equation as follows:

5 + 3 = 5 + 3

We simplify to get the following:

8 = 8

The equality still holds true as expected. Let’s try an example with one variable:

x – 2 = 13

We could add any number to both sides and the equation will still be true. However, it would make more sense to use a strategy that allows us to solve for x as follows:

x – 2 + 2 = 13 + 2

x = 15

By using the additive property of equality and adding 2 to both sides of the equation, we are able to find the value of x.

Addition Properties: There is an operation +, called addition, on Z satisfying aa) Addition is well defined, that is given any two integers a, b, a + b is uniquely defined. Thus, if a = b then a + c = b + c and c + a = c + b for any integer c. (Also, if a = b and c = d then a + c = b + d, c + a = d + b, a + d = b + c, d + a = c + b. We sometimes call this the substitution law.)

a) The set of integers is closed under addition. For any a, b ∈ Z, a + b ∈
b) Addition is commutative. For any a, b ∈ Z, a + b = b + a.
c) Addition is associative. For any a, b, c ∈ Z, (a + b) + c = a + (b + c).
d) There is a zero element 0 ∈ Z, satisfying 0 + a = a = a + 0 for any a ∈ e) For any a ∈ Z, there exists an additive inverse −a ∈ Z satisfying a + (−a) = 0 = (−a) + a. Definition: Subtraction in Z is defined by a − b = a + (−b) for a, b ∈ Z.

The field axioms are generally written in additive pairs.